题目内容
若a>0,b>0,且函数f(x)=4x3-ax2-2bx-2在x=1处有极值,则ab的最大值( )
| A、2 | B、3 | C、6 | D、9 |
考点:利用导数研究函数的极值
专题:计算题,导数的综合应用,不等式的解法及应用
分析:求出函数的导数,由极值的概念得到f′(1)=0,即有a+b=6,再由基本不等式即可得到最大值.
解答:
解:函数f(x)=4x3-ax2-2bx-2的导数f′(x)=12x2-2ax-2b,
由于函数f(x)=4x3-ax2-2bx-2在x=1处有极值,
则有f′(1)=0,即有a+b=6,(a,b>0),
由于a+b≥2
,即有ab≤(
)2=9,当且仅当a=b=3取最大值9.
故选D.
由于函数f(x)=4x3-ax2-2bx-2在x=1处有极值,
则有f′(1)=0,即有a+b=6,(a,b>0),
由于a+b≥2
| ab |
| a+b |
| 2 |
故选D.
点评:本题考查导数的运用:求极值,考查基本不等式的运用,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图是函数f(x)的导函数f′(x)的图象,则下面判断正确的是( )
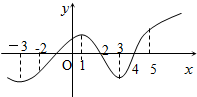
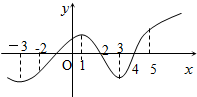
| A、函数f(x)在区间(-2,1)上单调递增 |
| B、函数f(x)在x=1处取得极大值 |
| C、函数f(x)在(4,5)上单调递增 |
| D、当x=4时,f(x)取极大值 |
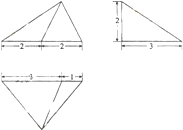 若某几何体的三视图(单位:cm)如图所示(依次为正视图、侧视图、俯视图),则此几何体的体积是
若某几何体的三视图(单位:cm)如图所示(依次为正视图、侧视图、俯视图),则此几何体的体积是