题目内容
若向量
=（1，λ，2），
=（2，-1，2）．
，
夹角的余弦值是
，则λ的值为（ ）
| a |
| b |
| a |
| b |
| 8 |
| 9 |
| A、2 | B、-2 | C、-3 | D、3 |
考点：空间向量的正交分解及其坐标表示
专题：计算题,空间位置关系与距离
分析：设向量
，
的夹角为θ，可得cosθ=
=
，解这个关于λ的方程即可．
| a |
| b |
| 6-λ | ||
3
|
| 8 |
| 9 |
解答：
解：设向量
，
的夹角为θ，则
∵向量
=（1，λ，2），
=（2，-1，2），
∴cosθ=
=
=
，
解得λ=-2，
故选B．
| a |
| b |
∵向量
| a |
| b |
∴cosθ=
| 2-λ+4 | ||||
|
| 6-λ | ||
3
|
| 8 |
| 9 |
解得λ=-2，
故选B．
点评：本题考查空间向量的夹角与距离公式，属基础题．
练习册系列答案
相关题目
十一黄金周期间，5位同学各自随机从“三峡明珠，山水宜昌”、“千古帝乡，智慧襄阳”、“养生山水，长寿钟祥”三个城市中选择一个旅游，则三个城市都有人选的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
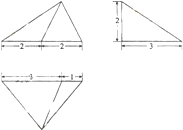若某几何体的三视图（单位：cm）如图所示（依次为正视图、侧视图、俯视图），则此几何体的体积是