题目内容
已知a=2log52,b=21.1,c=(
)-0.8,则a、b、c的大小关系是( )
| 1 |
| 2 |
| A、.a<c<b |
| B、c<b<a |
| C、a<b<c |
| D、b<c<a |
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:转化为同底数:a=2log52=log
<1,b=21.1,c=(
)-0.8=2
,根据函数y=2x单调性判断答案.
4 5 |
| 1 |
| 2 |
| 4 |
| 5 |
解答:
解:∵a=2log52,b=21.1,c=(
)-0.8,
∴a=2log52=log54<1,b=21.1>2,c=(
)-0.8=2
<2,1<c<2
根据函数y=2x单调性判断:b>c>a,
故选;A
| 1 |
| 2 |
∴a=2log52=log54<1,b=21.1>2,c=(
| 1 |
| 2 |
| 4 |
| 5 |
根据函数y=2x单调性判断:b>c>a,
故选;A
点评:本题考查了指数函数的单调性,属于容易题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
如图是函数f(x)的导函数f′(x)的图象,则下面判断正确的是( )
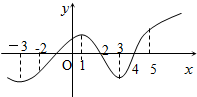
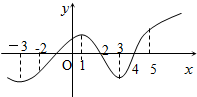
| A、函数f(x)在区间(-2,1)上单调递增 |
| B、函数f(x)在x=1处取得极大值 |
| C、函数f(x)在(4,5)上单调递增 |
| D、当x=4时,f(x)取极大值 |
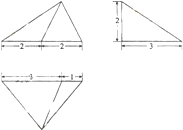 若某几何体的三视图(单位:cm)如图所示(依次为正视图、侧视图、俯视图),则此几何体的体积是
若某几何体的三视图(单位:cm)如图所示(依次为正视图、侧视图、俯视图),则此几何体的体积是