题目内容
设m,n是两条不同的直线,α,β是两个不同的平面,给出下列四个命题:
①如果m∥α,n?α,那么m∥n;
②如果m⊥α,m⊥β,那么α∥β;
③如果α⊥β,m⊥α,那么m∥β;
④如果α⊥β,α∩β=m,m⊥n,那么n⊥β.
其中正确的命题是( )
①如果m∥α,n?α,那么m∥n;
②如果m⊥α,m⊥β,那么α∥β;
③如果α⊥β,m⊥α,那么m∥β;
④如果α⊥β,α∩β=m,m⊥n,那么n⊥β.
其中正确的命题是( )
| A、① | B、② | C、③ | D、④ |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:①如果m∥α,n?α,m与n平行或异面,故①错误;
②如果m⊥α,m⊥β,那么由平面与平面平行的判定定理得α∥β,故②正确;
③如果α⊥β,m⊥α,那么m∥β或m?β,故③错误;
④如果α⊥β,α∩β=m,m⊥n,那么n与β相交,平行或n?β,故④错误.
故选:B.
②如果m⊥α,m⊥β,那么由平面与平面平行的判定定理得α∥β,故②正确;
③如果α⊥β,m⊥α,那么m∥β或m?β,故③错误;
④如果α⊥β,α∩β=m,m⊥n,那么n与β相交,平行或n?β,故④错误.
故选:B.
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知|lga|=lgb(a>0,b>0),那么( )
| A、a=b | B、a=b或ab=1 |
| C、a=±b | D、ab=1 |
十一黄金周期间,5位同学各自随机从“三峡明珠,山水宜昌”、“千古帝乡,智慧襄阳”、“养生山水,长寿钟祥”三个城市中选择一个旅游,则三个城市都有人选的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知二项式(2x2+
)n(n∈N*)展开式中,前三项的二项式系数和是56,则展开式中的常数项为( )
| 1 | ||
|
| A、180 | B、360 |
| C、1152 | D、2304 |
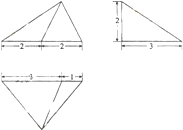 若某几何体的三视图(单位:cm)如图所示(依次为正视图、侧视图、俯视图),则此几何体的体积是
若某几何体的三视图(单位:cm)如图所示(依次为正视图、侧视图、俯视图),则此几何体的体积是