题目内容
15.已知实数x,y满足不等式组$\left\{\begin{array}{l}x+y-5≤0\\ x-2y+1≤0\\ x≥1\end{array}\right.$,若不等式y2-2xy≤ax2恒成立,则实数a的最小值为( )| A. | 8 | B. | 3 | C. | -1 | D. | -6 |
分析 作出不等式组对应的平面区域,利用不等式恒成立转化为最值问题,利用斜率的几何意义以及一元二次函数的性质进行转化求解即可.
解答 解:作出不等式组对应的平面区域如图: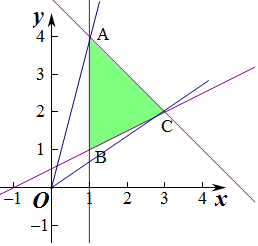
由图象知,x≥1,
则不等式y2-2xy≤ax2恒成立,等价为a≥($\frac{y}{x}$)2-2•($\frac{y}{x}$),
设k=$\frac{y}{x}$,则($\frac{y}{x}$)2-2•($\frac{y}{x}$)=k2-2k=(k-1)2-1,
k的几何意义是区域内的点到原点的斜率,
由图象知OC的斜率最小,OA的斜率最大,
由$\left\{\begin{array}{l}{x=1}\\{x+y-5=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,即A(1,4),
由$\left\{\begin{array}{l}{x+y-5=0}\\{x-2y+1=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$,即C(3,2),
则OA的斜率k=4,OC的斜率k=$\frac{2}{3}$,
则$\frac{2}{3}$≤k≤4,
则当k=4时,(k-1)2-1=9-1=8,
则($\frac{y}{x}$)2-2•($\frac{y}{x}$)的最大值为8,
则a≥8,
即a的最小值为8,
故选:A.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义以及不等式恒成立,利用参数分离法转化求求函数的最值是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列说法错误的是( )
| A. | 若命题p∧q为假命题,则p,q都是假命题 | |
| B. | 已知命题p:?x∈R,x2+x+1>0,则¬p:?x0∈R,x02+x0+1≤0 | |
| C. | 命题“若x2-3x+2=0,则x=1”的逆命题为:“若x≠1,则x2-3x+2≠0” | |
| D. | “x=1”是“x2-3x+2=0”的充分不必要条件 |
20.实数集R,设集合P={x|x2-4x+3≤0},Q={x|x2-4<0},则P∪(∁RQ)=( )
| A. | [2,3] | B. | (1,3) | C. | (2,3] | D. | (-∞,-2]∪[1,+∞) |
15.茎叶图如图1,为高三某班60名学生的化学考试成绩,算法框图如图2中输入的a1为茎叶图中的学生成绩,则输出的m,n分别是( )
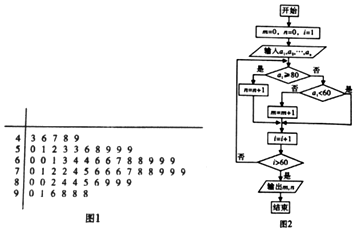

| A. | m=29,n=15 | B. | m=29,n=16 | C. | m=15,n=16 | D. | m=16,n=15 |