题目内容
3．设θ为锐角，若cos（θ+$\frac{3π}{16}$）=$\frac{3}{5}$，则sin（θ-$\frac{π}{16}$）=$\frac{\sqrt{2}}{10}$．分析 利用同角三角函数的基本关系、两角差的正弦公式，求得sin（θ-$\frac{π}{16}$）=sin[（θ+$\frac{3π}{16}$）-$\frac{π}{4}$]的值．
解答 解：∵θ为锐角，若cos（θ+$\frac{3π}{16}$）=$\frac{3}{5}$，则sin（θ+$\frac{3π}{16}$）=$\sqrt{{1-cos}^{2}（θ+\frac{3π}{16}）}$=$\frac{4}{5}$，
sin（θ-$\frac{π}{16}$）=sin[（θ+$\frac{3π}{16}$）-$\frac{π}{4}$]=sin（θ+$\frac{3π}{16}$）cos$\frac{π}{4}$-cos（θ+$\frac{3π}{16}$）•sin$\frac{π}{4}$
=$\frac{4}{5}•\frac{\sqrt{2}}{2}$-$\frac{3}{5}•\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{10}$，
故答案为：$\frac{\sqrt{2}}{10}$．
点评 本题主要考查同角三角函数的基本关系、两角差的正弦公式的应用，属于基础题．
练习册系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
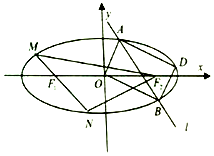已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），短轴长2，两焦点分别为F1，F2，过F1的直线交椭圆C于M，N两点，且△F2MN的周长为8．
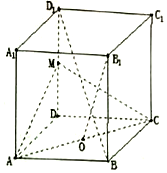在正方体ABCD-A1B1C1D1中，M为DD1的中点，O为AC的中点，AB=1．