题目内容
20.实数集R,设集合P={x|x2-4x+3≤0},Q={x|x2-4<0},则P∪(∁RQ)=( )| A. | [2,3] | B. | (1,3) | C. | (2,3] | D. | (-∞,-2]∪[1,+∞) |
分析 解不等式求得集合P、Q,再根据补集与并集的定义计算即可.
解答 解:实数集R,集合P={x|x2-4x+3≤0}={x|1≤x≤3},
Q={x|x2-4<0}={x|-2<x<2},
∴∁RQ={x|x≤-2或x≥2},
∴P∪(∁RQ)={x|x≤-2或x≥1}=(-∞,-2]∪[1,+∞).
故选:D.
点评 本题考查了解不等式与集合的运算问题,是基础题.

练习册系列答案
相关题目
15.已知实数x,y满足不等式组$\left\{\begin{array}{l}x+y-5≤0\\ x-2y+1≤0\\ x≥1\end{array}\right.$,若不等式y2-2xy≤ax2恒成立,则实数a的最小值为( )
| A. | 8 | B. | 3 | C. | -1 | D. | -6 |
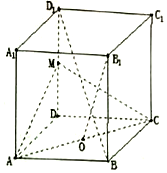 在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为AC的中点,AB=1.
在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为AC的中点,AB=1.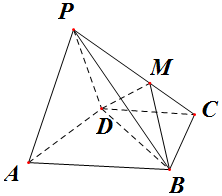 如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.
如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.