题目内容
已知函数f（x）=sin（4x+
）+cos（4x-
）．
（Ⅰ）求函数f（x）的最大值；
（Ⅱ）若直线x=m是曲线y=f（x）的对称轴，求实数m的值．
| π |
| 4 |
| π |
| 4 |
（Ⅰ）求函数f（x）的最大值；
（Ⅱ）若直线x=m是曲线y=f（x）的对称轴，求实数m的值．
考点：两角和与差的正弦函数,三角函数的最值
专题：三角函数的图像与性质
分析：（Ⅰ）利用两角和的三角公式，根据三角函数的性质即可求函数f（x）的最大值；
（Ⅱ）根据三角函数的对称性公式即可求出m的值．
（Ⅱ）根据三角函数的对称性公式即可求出m的值．
解答：
解：（Ⅰ）∵f（x）=sin（4x+
）+cos（4x-
）=sin（4x+
）+sin（4x+
）=2sin（4x+
），
∴f（x）的最大值是2．
（Ⅱ）令4x+
=
+kπ，（k∈Z），
则x=
+
，
而直线x=m是函y=f（x）的对称轴，
∴m=
+
，（k∈Z）．
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
∴f（x）的最大值是2．
（Ⅱ）令4x+
| π |
| 4 |
| π |
| 2 |
则x=
| kπ |
| 4 |
| π |
| 16 |
而直线x=m是函y=f（x）的对称轴，
∴m=
| kπ |
| 4 |
| π |
| 16 |
点评：本题主要考查三角函数的图象和性质，利用条件求出f（x）的表达式是解决本题的关键．
练习册系列答案
相关题目
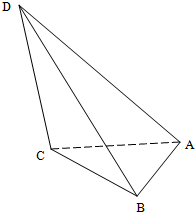在四面体ABCD中，AB=AC=1，∠BAC=90°，AD=