题目内容
已知函数f（x）=ex，g（x）=ax2+bx+1，当a=0时，若f（x）≥g（x）对任意x恒成立，求b的取值集合．
考点：函数恒成立问题
专题：函数的性质及应用
分析：令h（x）=ex-bx-1≥0对任意x恒成立，h'（x）=ex-b，由此利用导数性质能求出b的取值集合．
解答：
解：∵函数f（x）=ex，g（x）=ax2+bx+1，
当a=0时，f（x）≥g（x）对任意x恒成立，
令h（x）=ex-bx-1≥0对任意x恒成立，
h（x）=e^2-bx-1，当x=lnb取最小，最小值应为为b-blnb-1≥0，
令t（b）=b-blnb-1
t'（b）=1-b•
-lnb=-lnb=0时，
b=1，t（b）在（0，1）上单调递增，在（1，+∞）上单调递增，
所以t（b）max=t（1）=0
所以只有b=1时满足h（lnb）≥0，
所以b∈{1}．
当a=0时，f（x）≥g（x）对任意x恒成立，
令h（x）=ex-bx-1≥0对任意x恒成立，
h（x）=e^2-bx-1，当x=lnb取最小，最小值应为为b-blnb-1≥0，
令t（b）=b-blnb-1
t'（b）=1-b•
| 1 |
| b |
b=1，t（b）在（0，1）上单调递增，在（1，+∞）上单调递增，
所以t（b）max=t（1）=0
所以只有b=1时满足h（lnb）≥0，
所以b∈{1}．
点评：本题考查实数的取值范围的求法，是中档题，解题时要认真审题，注意导数性质和分类讨论思想的合理运用．
练习册系列答案
相关题目
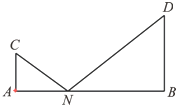如图，C，D是两个小区的所在地，C，D到一条公路AB的垂直距离CA=1km，DB=2km，AB两端之间的距离为4km．某公交公司将在AB之间找一点N，在N处建造一个公交站台．