题目内容
已知函数f（x）=ax2+bx+c（a≠0），判断并证明函数f（x）的单调性．
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：首先，求导数，然后，针对a的正负情形进行讨论，得到相应的单调区间．
解答：
解：∵f（x）=ax2+bx+c（a≠0），
∴f′（x）=2ax+b．
当a＞0时，令f'（x）＞0，解得x＞-
，
对应的增区间为（-
，+∞），
令f'（x）＜0，解得x＜-
，
对应的减区间为（-∞，-
，），
当a＜0时，令f'（x）＞0，解得x＜-
，
对应的增区间为（-∞，-
，），
令f'（x）＜0，解得x＞-
，
对应的减区间为（-
，+∞）．
∴f′（x）=2ax+b．
当a＞0时，令f'（x）＞0，解得x＞-
| b |
| 2a |
对应的增区间为（-
| b |
| 2a |
令f'（x）＜0，解得x＜-
| b |
| 2a |
对应的减区间为（-∞，-
| b |
| 2a |
当a＜0时，令f'（x）＞0，解得x＜-
| b |
| 2a |
对应的增区间为（-∞，-
| b |
| 2a |
令f'（x）＜0，解得x＞-
| b |
| 2a |
对应的减区间为（-
| b |
| 2a |
点评：本题重点考查了函数的单调性的判断与证明，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
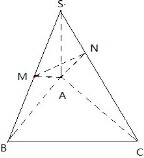在三棱锥S-ABC中，SA⊥底面ABC，∠ABC=90°，且SA=AB，点M是SB的中点，AN⊥SC且交SC于点N．