题目内容
若函数f（x）=ax3-bx+4，当x=2时，函数f（x）有极值，且函数f（x）图象上以点A（3，f（3））为切点的切线与直线5x-y+1=0平行．
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调区间；
（3）若方程f（x）=k有3个解，求实数k的取值范围．
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调区间；
（3）若方程f（x）=k有3个解，求实数k的取值范围．
考点：利用导数研究函数的极值,函数的零点与方程根的关系,利用导数研究函数的单调性
专题：计算题,导数的综合应用
分析：（1）求出导数，切线的斜率，由f′（2）=0，且f′（3）=5，列出方程，求出a，b即可；
（2）由（1）得，f'（x）=x2-4，令f'（x）=0，得x=2，或x=-2，列表求出单调区间和极值；
（3）由（2）画出函数f（x）的图象，及直线y=k，由图象观察即可．
（2）由（1）得，f'（x）=x2-4，令f'（x）=0，得x=2，或x=-2，列表求出单调区间和极值；
（3）由（2）画出函数f（x）的图象，及直线y=k，由图象观察即可．
解答：
解：（1）∵函数f（x）=ax3-bx+4，∴f′（x）=3ax2-b，
直线5x-y+1=0的斜率为5，
则由题意得，f′（2）=0，且f′（3）=5，即有12a-b=0且27a-b=5，
解得a=
，b=4，
∴f(x)=
x3-4x+4．
（2）由（1）得，f'（x）=x2-4，令f'（x）=0，得x=2，或x=-2．
当x变化时，f'（x），f（x）的变化情况如下表：
则函数f（x）的单调增区间为（-∞，-2），（2，+∞），单调减区间为（-2，2）．
（3）由（2）得f（x）的极大值为f（-2）=
，极小值为f（2）=-
．
函数f(x)=
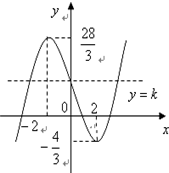
x3-4x+4的图象大致如右：
若方程f（x）=k有3个解，需使直线y=k与函数
f(x)=
x3-4x+4的图象有3个交点，
由图象可知：-
＜k＜
．
解：（1）∵函数f（x）=ax3-bx+4，∴f′（x）=3ax2-b，直线5x-y+1=0的斜率为5，
则由题意得，f′（2）=0，且f′（3）=5，即有12a-b=0且27a-b=5，
解得a=
| 1 |
| 3 |
∴f(x)=
| 1 |
| 3 |
（2）由（1）得，f'（x）=x2-4，令f'（x）=0，得x=2，或x=-2．
当x变化时，f'（x），f（x）的变化情况如下表：
| x | （-∞，-2） | -2 | （-2，+2） | 2 | （2，+∞） | ||||
| f'（x） | + | 0 | - | 0 | + | ||||
| f（x） | ↗ |
| ↘ | -
| ↗ |
（3）由（2）得f（x）的极大值为f（-2）=
| 28 |
| 3 |
| 4 |
| 3 |
函数f(x)=
| 1 |
| 3 |
若方程f（x）=k有3个解，需使直线y=k与函数
f(x)=
| 1 |
| 3 |
由图象可知：-
| 4 |
| 3 |
| 28 |
| 3 |
点评：本题考查导数的综合应用：求切线方程和求单调区间和极值，考查数形结合的能力，以及运算能力，属于基础题．
练习册系列答案
相关题目