题目内容
两个单位向量
,
的夹角为θ,且θ∈(
,
),则
+
与λ
(λ>0)夹角的范围是 .
| a |
| b |
| π |
| 6 |
| π |
| 3 |
| a |
| b |
| b |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:利用数量积运算和向量的夹角公式、余弦函数的单调性即可得出.
解答:
解:∵两个单位向量
,
的夹角为θ,且θ∈(
,
),
∴cosθ=
=
•
∈(
,
),|
+
|=
=
.
设
+
与λ
(λ>0)夹角为α,
•
=t.
则cosα=
=
=
=
=
,
∵t∈(
,
),∴
∈(
,
),即
∈(
,
).
∴
+
与λ
(λ>0)夹角的范围是(
,
).
故答案为:(
,
).
| a |
| b |
| π |
| 6 |
| π |
| 3 |
∴cosθ=
| ||||
|
|
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
|
2+2
|
设
| a |
| b |
| b |
| a |
| b |
则cosα=
(
| ||||||
|
|
λ
| ||||||
|
λ
| ||||||
|
| t+1 | ||
|
| ||
|
∵t∈(
| 1 |
| 2 |
| ||
| 2 |
| ||
|
| ||
| 2 |
| ||||
| 2 |
| ||
|
| ||
| 2 |
| ||||
| 4 |
∴
| a |
| b |
| b |
| ||
| 2 |
| ||||
| 4 |
故答案为:(
| ||
| 2 |
| ||||
| 4 |
点评:本题考查了数量积运算和向量的夹角公式、余弦函数的单调性,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
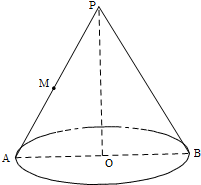 已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,底面半径OC与母线PB所成的角的大小等于θ.
已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,底面半径OC与母线PB所成的角的大小等于θ.