题目内容

若数列{an}的前n项和Sn=n2+3n，则a6+a7+a8=
 
．
考点：数列的求和
专题：等差数列与等比数列
分析：利用公式n≥2时，an=sn-sn-1，即可求得结论．
解答： 解：由题意得
a6+a7+a8=s8-s5=（82+3×8）-（52+3×5）=88-40=48．
故答案为：48．
点评：本题主要考查数列公式n≥2时，an=sn-sn-1，的运用，属基础题．
练习册系列答案
相关题目
有以下四个命题：
①对于任意实数a、b、c，若a＞b，c≠0，则ac＞bc；
②设Sn是等差数列{an}的前n项和，若a2+a6+a10为一个确定的常数，则S11也是一个确定的常数；
③在三角形△ABC中，若sinA＞sinB，恒有A＞B；
④对于任意正实数x，若sinx＞0，y=sinx+
2
sinx
，则y的最小值为2
2
．
其中正确命题的是
 
（把正确的答案题号填在横线上）
两个单位向量
a
，
b
的夹角为θ，且θ∈（
π
6
，
π
3
），则
a
+
b
与λ
b
（λ＞0）夹角的范围是
 
．
不等式组
x-y+2≥0
x+y≥0
x≤2
表示的平面区域的面积为
 
．
如图，CD、BE是△ABC的高，且相交于点F．若BF=FE，且FC=4FD=4，则FE=
 
，∠A=
 
．
用秦九韶算法计算多项式f（x）=3x6+4x5+5x4+6x3+7x2+8x+1当x=0.7时的值时，需要做乘法和加法运算的次数共
 
次．
设集合u={（x，y）|x∈R，y∈R}，A={（x，y）|2x-y+m＞0}，B={（x，y）|x+y-n≤0}，那么点P（2，3）∈A∩（∁UB）的充要条件是
 
．
函数y=lnx-x的单调增区间为
 
．
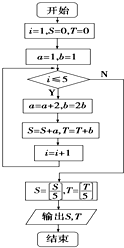阅读程序框图设[x]表示取x的整数部分，如[5]=5，[2.7]=2，经过程序框图运行后输出结果为S，T，设z1=S-Ti，z2=1+i，z=z1•z2，则|z|=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网