题目内容

在数列{an}中，a1=6，
an+1
an
=
n+3
n
，那么{an}的通项公式是
 
．
考点：数列的函数特性
专题：点列、递归数列与数学归纳法
分析：利用“累乘求积法”即可得出．
解答： 解：∵在数列{an}中，a1=6，
an+1
an
=
n+3
n
，
∴当n≥4时，an=
an
an-1
•
an-1
an-2
•
an-2
an-3
•…•
a4
a3
•
a3
a2
•
a2
a1
•a1
=
n+2
n-1
•
n+1
n-2
•
n
n-3
•
n-1
n-4
•…•
3+3
3
•
2+3
2
•
1+3
1
×6
=n（n+1）（n+2），
经验证当n=1，2，3时也成立，
因此：an=n（n+1）（n+2）．
故答案为：an=n（n+1）（n+2）．
点评：本题考查了“累乘求积法”，属于基础题．
练习册系列答案
相关题目
两个单位向量
a
，
b
的夹角为θ，且θ∈（
π
6
，
π
3
），则
a
+
b
与λ
b
（λ＞0）夹角的范围是
 
．
设集合u={（x，y）|x∈R，y∈R}，A={（x，y）|2x-y+m＞0}，B={（x，y）|x+y-n≤0}，那么点P（2，3）∈A∩（∁UB）的充要条件是
 
．
函数y=lnx-x的单调增区间为
 
．
已知12a=3b=2，则
1
a
-
1
b
=
 
．
已知函数f（x）=sin（ωx+
π
4
），若f（
π
2
）=f（π），且在区间（
π
2
，π）内f（x）≤f（
π
2
），则ω=
 
．
圆台的母线长是3，侧面展开后所得扇环的圆心角为180°，侧面积为10π，则圆台的高为
 
，上下底面的半径为
 
．
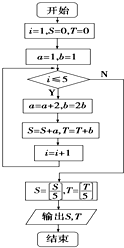阅读程序框图设[x]表示取x的整数部分，如[5]=5，[2.7]=2，经过程序框图运行后输出结果为S，T，设z1=S-Ti，z2=1+i，z=z1•z2，则|z|=
 
．
已知a=log1.20.3，b=log1.20.8，c=1.50.5，则a，b，c的大小关系为（　　）
A、a＞b＞c
B、c＞a＞b
C、a＞c＞b
D、c＞b＞a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网