题目内容
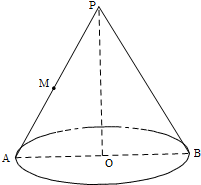 已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,底面半径OC与母线PB所成的角的大小等于θ.
已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,底面半径OC与母线PB所成的角的大小等于θ.(1)当θ=60°时,求异面直线MC与PO所成的角的余弦值;
(2)当三棱锥M-ACO的体积最大时,求θ的值.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)首先,作辅助线:连MO,过M作MD⊥AO交AO于点D,连DC,然后,得到∠DMC或其补角即为所求,最后,求解即可;
(2)借助于体积公式,分析得到:当OC⊥OA时,△OCA的面积最大,进一步求解即可.
(2)借助于体积公式,分析得到:当OC⊥OA时,△OCA的面积最大,进一步求解即可.
解答:
解:(1)连MO,过M作MD⊥AO交AO于点D,连DC.
又PO=
=2
,∴MD=
.又OC=4,OM=3.
∵MD∥PO,∴∠DMC等于异面直线MC与PO所成的角或其补角.
∵MO∥PB,∴∠MOC=60°或120°.
当∠MOC=60°时,
∴MC=
.
∴cos∠DMC=
=
,
当∠MOC=120°时,
∴MC=
.
∴cos∠DMC=
=
,
综上,异面直线MC与PO所成的角余弦值等于
cos∠DMC=
=
或cos∠DMC=
=
.
(2)∵三棱锥M-ACO的高为MD且长为
,
要使得三棱锥M-ACO的体积最大只要底面积△OCA的面积最大.
而当OC⊥OA时,△OCA的面积最大.
又OC⊥OP,此时OC⊥平面PAB,
∴OC⊥PB,θ=90°.
又PO=
| 62-42 |
| 5 |
| 5 |
∵MD∥PO,∴∠DMC等于异面直线MC与PO所成的角或其补角.
∵MO∥PB,∴∠MOC=60°或120°.

当∠MOC=60°时,
∴MC=
| 13 |
∴cos∠DMC=
| MD |
| MC |
| ||
| 13 |
当∠MOC=120°时,
∴MC=
| 37 |
∴cos∠DMC=
| MD |
| MC |
| ||
| 37 |
综上,异面直线MC与PO所成的角余弦值等于
cos∠DMC=
| MD |
| MC |
| ||
| 37 |
| MD |
| MC |
| ||
| 13 |
(2)∵三棱锥M-ACO的高为MD且长为
| 5 |
要使得三棱锥M-ACO的体积最大只要底面积△OCA的面积最大.
而当OC⊥OA时,△OCA的面积最大.
又OC⊥OP,此时OC⊥平面PAB,
∴OC⊥PB,θ=90°.
点评:本题重点考查了异面直线所成的角、棱锥的体积计算、空间中垂直关系和平行关系等知识,属于中档题.

练习册系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF