题目内容
已知sin(π-α)=-2sin(
+α),则
= .
| π |
| 2 |
| sinα+cosα |
| sinα-cosα |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:已知等式左右两边利用诱导公式化简,求出tanα的值,原式分子分母除以cosα,利用同角三角函数间基本关系弦化切后,将tanα的值代入计算即可求出值.
解答:
解:∵sin(π-α)=-2sin(
+α),
∴sinα=-2cosα,即tanα=-2,
则原式=
=
=
.
故答案为:
.
| π |
| 2 |
∴sinα=-2cosα,即tanα=-2,
则原式=
| tanα+1 |
| tanα-1 |
| -2+1 |
| -2-1 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF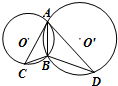 如图,圆O与圆O′相交于A、B两点,AD与AC分别是圆O与圆O′的A点处的切线.若BD=2BC=2,则AB=
如图,圆O与圆O′相交于A、B两点,AD与AC分别是圆O与圆O′的A点处的切线.若BD=2BC=2,则AB=