题目内容
设函数f(x)=sin(ωx+
)(ω>0)与函数g(x)=cos(2x+φ)(|φ|≤
)的对称轴完全相同,则φ的值为( )
| π |
| 4 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:根据题意,求出两个函数的对称轴,利用对称轴完全相同,求出ϕ的值.
解答:
解:由题意,∵函数g(x)=cos(2x+φ)(|φ|≤
),
令2x+φ=kπ,
∴对称轴x=
(k∈Z);
∵函数f(x)=2sin(ωx+
),
令ωx+
=mπ+
,
∴对称轴x=
(m∈Z);
又∵函数f(x)与函数g(x)的对称轴完全相同,
∴ω=2,φ=-
.
故选:B.
| π |
| 2 |
令2x+φ=kπ,
∴对称轴x=
| kπ-φ |
| 2 |
∵函数f(x)=2sin(ωx+
| π |
| 4 |
令ωx+
| π |
| 4 |
| π |
| 2 |
∴对称轴x=
mπ+
| ||
| ω |
又∵函数f(x)与函数g(x)的对称轴完全相同,
∴ω=2,φ=-
| π |
| 4 |
故选:B.
点评:本题考查了三角函数的图象与性质的应用问题,也考查一定的运算与化简能力,是基础题.

练习册系列答案
相关题目
(
+
)50的二项展开式中,整数项的个数是( )
| 3 | 2 |
| 1 | ||
|
| A、3 | B、4 | C、5 | D、6 |
α=-
,则角α的终边在( )
| 2π |
| 3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知x、y的取值如下表所示:
从散点图分析、y与x线性相关,且
=0.95x+2.6,则m的值为( )
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | m |
 |
| y |
| A、6.4 | B、6.5 |
| C、6.7 | D、6.8 |
已知奇函数f(x)在x≥0时,f(x)=x2-4x,则使f(x-2)>-3成立的x的取值范围是( )
A、(-2-
| ||
B、(-4-
| ||
C、(-
| ||
D、(-∞,-
|
某设备零件的三视图如图所示,则这个零件的体积为( )


| A、6 | B、8 | C、3 | D、4 |
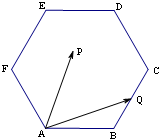 如图,在正六边形ABCDEF中,AB=2,点Q为BC边的中点,点P在正六边形ABCDEF内(含边界),则
如图,在正六边形ABCDEF中,AB=2,点Q为BC边的中点,点P在正六边形ABCDEF内(含边界),则 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点.
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点.