题目内容
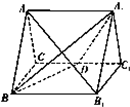 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.(Ⅰ)求证:AB1⊥A1D;
(Ⅱ)求点C到平面A1BD的距离.
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:几何法:
(Ⅰ)取BC中点O,连结AO,由正三角形的性质得AO⊥BC.由线面垂直的AO⊥BD,由正方形的性质得B1O⊥BD从而得到BD⊥AB1,由此能证明AB1⊥A1D.
(Ⅱ)由题意知S△A1BD=
,S△BCD=1.A1到平面BCC1B1的距离为
,由此利用等积法能求出点C到平面A1BD的距离.
向量法:
(Ⅰ)取B1C1中点O1,以O为原点,
,
,
的方向为x,y,z轴的正方向,建立空间直角坐标系,利用向量法能证明AB1⊥A1D.
(Ⅱ)求出平面A1BD的法向量和
,由此利用向量法能求出点C到平面A1BD的距离.
(Ⅰ)取BC中点O,连结AO,由正三角形的性质得AO⊥BC.由线面垂直的AO⊥BD,由正方形的性质得B1O⊥BD从而得到BD⊥AB1,由此能证明AB1⊥A1D.
(Ⅱ)由题意知S△A1BD=
| 6 |
| 3 |
向量法:
(Ⅰ)取B1C1中点O1,以O为原点,
| OB |
| OO1 |
| OA |
(Ⅱ)求出平面A1BD的法向量和
| BC |
解答:
几何法:
(Ⅰ)证明:取BC中点O,连结AO.
∵△ABC为正三角形,∴AO⊥BC.
∵正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,
∴AO⊥平面BCC1B1,∴AO⊥BD.
连结B1O,在正方形BB1C1C中,O,D分别为BC,CC1的中点,∴B1O⊥BD.
∴BD⊥平面AB1O.∴BD⊥AB1.(4分 )
又在正方形ABB1A1中,AB1⊥A1B,又BD∩A1B=B,
∴AB1⊥平面A1BD.∴AB1⊥A1D.(6分)
(Ⅱ)解:△A1BD中,BD=A1D=
,A1B=2
,
∴S△A1BD=
,S△BCD=1.
在正三棱柱中,A1到平面BCC1B1的距离为
.(9分)
设点C到平面A1BD的距离为d.
由VA1-BCD=VC-A1BD得
S△BCD•
=
S△A1BD•d,(10分)
∴d=
=
.
∴点C到平面A1BD的距离为
.(12分)
向量法:
(Ⅰ)证明:取BC中点O,连结AO.
∵△ABC为正三角形,∴AO⊥BC.
∵在正三棱柱ABC-A1B1C1中,
平面ABC⊥平面BCC1B1,∴AD⊥平面BCC1B1.
取B1C1中点O1,以O为原点,
,
,
的方向为x,y,z轴的正方向,
建立空间直角坐标系,
则B(1,0,0),D(-1,1,0),
A1(0,2,
),A(0,0,
),B1(1,2,0),(4分)
∴
=(1,2,-
),
=(-1,-1,-
).
∵
•
=-1-2+3=0,∴
⊥
.
∴AB1⊥A1D.(6分)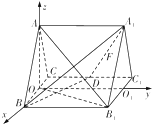
(Ⅱ)解:设平面A1BD的法向量为
=(x,y,z).
=(-1,-1,-
),
=(-2,1,0).
∵
⊥
,
⊥
,
∴
,∴
令x=1,得
=(1,2,-
)为平面A1BD的一个法向量.(9分)
∵
=(-2,0,0),
∴点C到平面A1BD的距离d=
=
=
.(12分).
(Ⅰ)证明:取BC中点O,连结AO.
∵△ABC为正三角形,∴AO⊥BC.
∵正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,
∴AO⊥平面BCC1B1,∴AO⊥BD.
连结B1O,在正方形BB1C1C中,O,D分别为BC,CC1的中点,∴B1O⊥BD.
∴BD⊥平面AB1O.∴BD⊥AB1.(4分 )
又在正方形ABB1A1中,AB1⊥A1B,又BD∩A1B=B,
∴AB1⊥平面A1BD.∴AB1⊥A1D.(6分)
(Ⅱ)解:△A1BD中,BD=A1D=
| 5 |
| 2 |
∴S△A1BD=
| 6 |
在正三棱柱中,A1到平面BCC1B1的距离为
| 3 |
设点C到平面A1BD的距离为d.
由VA1-BCD=VC-A1BD得
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
∴d=
| ||
| S△A1BD |
| ||
| 2 |
∴点C到平面A1BD的距离为
| ||
| 2 |
向量法:
(Ⅰ)证明:取BC中点O,连结AO.
∵△ABC为正三角形,∴AO⊥BC.
∵在正三棱柱ABC-A1B1C1中,
平面ABC⊥平面BCC1B1,∴AD⊥平面BCC1B1.
取B1C1中点O1,以O为原点,
| OB |
| OO1 |
| OA |
建立空间直角坐标系,
则B(1,0,0),D(-1,1,0),
A1(0,2,
| 3 |
| 3 |
∴
| AB1 |
| 3 |
| A1D |
| 3 |
∵
| AB1 |
| A1D |
| AB1 |
| A1D |
∴AB1⊥A1D.(6分)

(Ⅱ)解:设平面A1BD的法向量为
| n |
| A1D |
| 3 |
| BD |
∵
| n |
| A1D |
| n |
| BD |
∴
|
|
令x=1,得
| n |
| 3 |
∵
| BC |
∴点C到平面A1BD的距离d=
|
| ||||
|
|
| |-2| | ||
2
|
| ||
| 2 |
点评:本题考查异面直线垂直的证明,考查点到平面的距离的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
α=-
,则角α的终边在( )
| 2π |
| 3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
某设备零件的三视图如图所示,则这个零件的体积为( )


| A、6 | B、8 | C、3 | D、4 |
若实数a,b,c,d满足a>b,c>d,则下列不等式成立的是( )
| A、a-c>b-d | ||||
| B、a+c>b+d | ||||
| C、ac>bd | ||||
D、
|
过点P(3,2),且在两坐标轴上的截距相等的直线方程为( )
| A、2x-3y=0 |
| B、x+y-6=0 |
| C、x+y-5=0 |
| D、2x-3y=0或x+y-5=0 |
 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点.
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点. 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N.