题目内容
12.已知函数f(x)=3sin(ωx-$\frac{π}{6}$)(ω>0)和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.则f($\frac{π}{6}$)=$\frac{3}{2}$.分析 根据题意,得出函数f(x)和g(x)的周期相同,由此求出ω的值,写出f(x)的解析式,再求f($\frac{π}{6}$)的值.
解答 解:∵函数f(x)和g(x)图象的对称轴完全相同,
∴两个函数的周期相同,故ω=2;
∴函数f(x)=3sin(2x-$\frac{π}{6}$),
∴f($\frac{π}{6}$)=3sin(2×$\frac{π}{6}$-$\frac{π}{6}$)=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了正弦型函数和余弦型函数的对称性问题,根据两个函数的对称轴完全相同,判断出两个函数的周期一致,从而求出ω的值,是解答本题的关键.

练习册系列答案
相关题目
4.下列函数中周期为$\frac{π}{2}$的偶函数是( )
| A. | y=sin4x | B. | y=cos22x-sin22x | C. | y=tan2x | D. | y=cos2x |
1.(1+x)+(1+x)2+(1+x)3+(1+x)4+…+(1+x)49展开式中x3的系数是( )
| A. | ${C}_{51}^{3}$ | B. | ${C}_{50}^{4}$ | C. | ${C}_{51}^{4}$ | D. | ${C}_{47}^{4}$ |
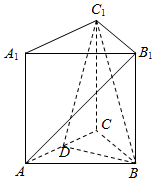 如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,CC1=AB=AC=BC=4,D为线段AC的中点.
如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,CC1=AB=AC=BC=4,D为线段AC的中点.