题目内容
4.已知点M是边长为2的正方形ABCD的内切圆内(含边界)一动点,则$\overrightarrow{MA}$•$\overrightarrow{MB}$的取值范围是( )| A. | [-1,0] | B. | [-1,2] | C. | [-1,3] | D. | [-1,4] |
分析 如图所示,由题意可得:点M所在的圆的方程为:(x-1)2+(y-1)2≤1(0≤x≤2,0≤y≤2).可设点M(x,y)可得$\overrightarrow{MA}$•$\overrightarrow{MB}$=(x-1)2+y2-1,由$\sqrt{(x-1)^{2}+{y}^{2}}$∈[0,2],即可得出.
解答  解:如图所示,
解:如图所示,
由题意可得:点M所在的圆的方程为:(x-1)2+(y-1)2≤1(0≤x≤2,0≤y≤2).
可设点M(x,y)
A(0,0),B(2,0).
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$=(-x,-y)•(2-x,-y)=-x(2-x)+y2=(x-1)2+y2-1,
由$\sqrt{(x-1)^{2}+{y}^{2}}$∈[0,2],
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$∈[-1,3],
故选:C.
点评 本题考查了圆的标准方程、向量数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列选项中是函数f(x)=sinx-$\sqrt{3}$cosx的零点的是( )
| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{7π}{6}$ | D. | $\frac{4π}{3}$ |
9.已知x,y满足约柬条件$\left\{\begin{array}{l}{x-y-1≤0}\\{2x-y-3≥0}\end{array}\right.$,当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2时,则$\frac{3}{a}$+$\frac{2}{b}$的最小值为( )
| A. | $\frac{25}{6}$ | B. | 4$+\sqrt{3}$ | C. | 4$+2\sqrt{3}$ | D. | 4$\sqrt{3}$ |
16.下列各组函数中,表示同一函数的是( )
| A. | y=$\sqrt{{x}^{2}}$和y=$(\sqrt{x})^{2}$ | B. | y=lg(x2-1)和y=lg(x+1)+lg(x-1) | ||
| C. | y=logax2和y=2logx | D. | y=x和y=logaax |
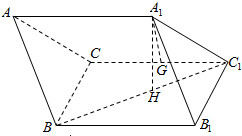 在三棱柱ABC-A1B1C1中,面BB1C1C是边长为2的正方形,点A1在平面BB1C1C上的射影H是BC1的中点,且A1H=$\sqrt{3}$,G是CC1的中点.
在三棱柱ABC-A1B1C1中,面BB1C1C是边长为2的正方形,点A1在平面BB1C1C上的射影H是BC1的中点,且A1H=$\sqrt{3}$,G是CC1的中点.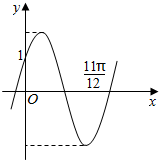 函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示
函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示