题目内容
15.下列选项中是函数f(x)=sinx-$\sqrt{3}$cosx的零点的是( )| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{7π}{6}$ | D. | $\frac{4π}{3}$ |
分析 由条件利用两角差的正弦公式化简函数的解析式,再利用函数的零点的定义求得函数的零点.
解答 解:函数f(x)=sinx-$\sqrt{3}$cosx=2sin(x-$\frac{π}{3}$),令f(x)=0,求得sin(x-$\frac{π}{3}$)=0,
经过检验,只有D满足条件,
故选:D.
点评 本题主要考查两角差的正弦公式,函数的零点的定义,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知函数f(x)=log2x,若在[1,8]上任取一个实数x0,则不等式1≤f(x0)≤2成立的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{7}$ | D. | $\frac{2}{5}$ |
10.下列函数中,既是奇函数又是增函数的为( )
| A. | y=-x2 | B. | $y=\frac{-1}{x}$ | C. | $y=x+\frac{1}{x}$ | D. | y=x|x| |
4.已知点M是边长为2的正方形ABCD的内切圆内(含边界)一动点,则$\overrightarrow{MA}$•$\overrightarrow{MB}$的取值范围是( )
| A. | [-1,0] | B. | [-1,2] | C. | [-1,3] | D. | [-1,4] |
5.已知直线2x+y-3=0的倾斜角为θ,则$\frac{sinθ+cosθ}{sinθ-cosθ}$的值是( )
| A. | -3 | B. | -2 | C. | $\frac{1}{3}$ | D. | 3 |
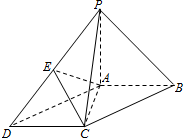 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.