题目内容
14.(1)计算log25625+lg0.01+ln$\sqrt{e}$-2;(2)已知tan(π+α)=3,求$\frac{2cos(π-a)-3sin(π+a)}{4cos(-a)+sin(2π-a)}$的值.
分析 (1)直接利用对数运算法则化简求解即可.
(2)利用诱导公式化简所求表达式为正切函数的形式,然后求出结果.
解答 解:(1)log25625+lg0.01+ln$\sqrt{e}$-2=2-2+$\frac{1}{2}$-2=-1.5…(5分)
(2)由已知得:tana=-3 …(7分)
$\frac{2cos(π-a)-3sin(π+a)}{4cos(-a)+sin(2π-a)}$=$\frac{-2cosα+3sinα}{4cosα-sinα}=\frac{-2+3tanα}{4-tanα}=-\frac{11}{7}$…(10分)
点评 本题考查三角函数的化简求值诱导公式的应用,对数的运算法则的应用,考查计算能力.

练习册系列答案
相关题目
3.已知函数f(x)=log2x,若在[1,8]上任取一个实数x0,则不等式1≤f(x0)≤2成立的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{7}$ | D. | $\frac{2}{5}$ |
4.已知点M是边长为2的正方形ABCD的内切圆内(含边界)一动点,则$\overrightarrow{MA}$•$\overrightarrow{MB}$的取值范围是( )
| A. | [-1,0] | B. | [-1,2] | C. | [-1,3] | D. | [-1,4] |
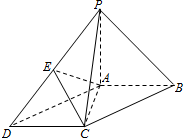 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.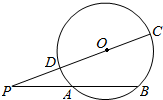 自圆O外一点P引圆O的两条割线PAB和PDC,如图所示,其中割线PDC过圆心O.AB=$\sqrt{2}$OA,PD=$\sqrt{3}$,∠P=15°,
自圆O外一点P引圆O的两条割线PAB和PDC,如图所示,其中割线PDC过圆心O.AB=$\sqrt{2}$OA,PD=$\sqrt{3}$,∠P=15°,