题目内容
5.已知函数f(x)=x3+ax2+x+1存在单调递减区间,则实数α的取值范围为( )| A. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | B. | [-$\sqrt{3}$,$\sqrt{3}$] | C. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
分析 由函数确定出导函数后,分析导函数的性质.由原函数有递减区间知导函数有小于0部分.
解答 解:∵f(x)=x3+ax2+x+1
∴f′(x)=3x2+2ax+1
∵函数f(x)存在单调减区间.
∴导函数f′(x)存在小于0部分,
∴△>0
∴a2>3
∴a>$\sqrt{3}$或a<-$\sqrt{3}$
∴a的取值范围为(-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞)
故选:A
点评 本题考查函数求导取得单调区间,以及二次函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知函数$f(x)=\left\{\begin{array}{l}sin(\frac{π}{2}x)-1,x<0\\{log_a}x(a>0,a≠1),x>0\end{array}\right.$的图象上关于y轴对称的点至少有5对,则实数的取值范围是( )
| A. | .$(0,\frac{{\sqrt{5}}}{5})$ | B. | $(\frac{{\sqrt{5}}}{5},1)$ | C. | $(0,\frac{1}{3})$ | D. | $(\frac{1}{3},1)$ |
20.已知等比数列{an}为递增数列,其前n项和为Sn,若S3=7,a2=2,则a3+a4+a5=( )
| A. | $\frac{7}{4}$ | B. | $\frac{7}{8}$ | C. | 28 | D. | 56 |
14.锐角△ABC中,a,b,c分别是角A,B,C的对边,若B=2A,则$\frac{b}{a}$的取值范围是( )
| A. | (0,2) | B. | ($\sqrt{2}$,2) | C. | ($\sqrt{2}$,$\sqrt{3}$) | D. | ($\sqrt{3}$,2) |
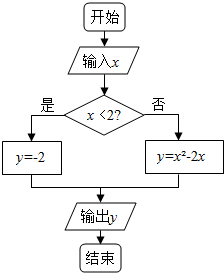 据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题
据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题