题目内容
14.锐角△ABC中,a,b,c分别是角A,B,C的对边,若B=2A,则$\frac{b}{a}$的取值范围是( )| A. | (0,2) | B. | ($\sqrt{2}$,2) | C. | ($\sqrt{2}$,$\sqrt{3}$) | D. | ($\sqrt{3}$,2) |
分析 由于B=2A,A,B为锐角,可得$\frac{π}{2}$<3A<π,$0>2A<\frac{π}{2}$,因此$\frac{π}{6}<A<\frac{π}{4}$,再利用正弦定理与倍角公式即可得出.
解答 解:∵B=2A,A,B为锐角,
∴$\frac{π}{2}$<3A<π,$0>2A<\frac{π}{2}$,∴$\frac{π}{6}<A<\frac{π}{4}$,
则$\frac{b}{a}$=$\frac{sinB}{sinA}$=$\frac{sin2A}{sinA}$=2cosA∈($\sqrt{2}$,$\sqrt{3}$),
故选:C.
点评 本题考查了倍角公式与正弦定理、三角形内角和定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
4. 我国古代数学名著《九章算数》中的更相减损法的思路与如图相似.记R(a\b)为a除以b所得余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出的b的值为( )
我国古代数学名著《九章算数》中的更相减损法的思路与如图相似.记R(a\b)为a除以b所得余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出的b的值为( )
 我国古代数学名著《九章算数》中的更相减损法的思路与如图相似.记R(a\b)为a除以b所得余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出的b的值为( )
我国古代数学名著《九章算数》中的更相减损法的思路与如图相似.记R(a\b)为a除以b所得余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出的b的值为( )| A. | 0 | B. | 1 | C. | 9 | D. | 18 |
5.已知函数f(x)=x3+ax2+x+1存在单调递减区间,则实数α的取值范围为( )
| A. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | B. | [-$\sqrt{3}$,$\sqrt{3}$] | C. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
9.已知0<x<8,则x(8-x)的最大值是( )
| A. | 7 | B. | 12 | C. | 15 | D. | 16 |
6.已知$\frac{sinα}{1+cosα}$=-$\frac{2}{3}$,则$\frac{sinα}{1-cosα}$的值是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
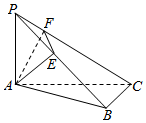 如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证:
如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证: