题目内容
15．y=sinxcosx的值域为[-$\frac{1}{2}$，$\frac{1}{2}$]，周期为π．分析 使用二倍角公式得出y=$\frac{1}{2}$sin2x．
解答 解：y=sinxcosx=$\frac{1}{2}$sin2x．
∴函数y的值域为[-$\frac{1}{2}$，$\frac{1}{2}$]．
周期T=$\frac{2π}{2}$=π．
故答案为[-$\frac{1}{2}$，$\frac{1}{2}$]，π．
点评 本题考查了正弦函数的图象与性质，属于基础题．
练习册系列答案
相关题目
5．已知函数f（x）=x3+ax2+x+1存在单调递减区间，则实数α的取值范围为（ ）
| A． | （-∞，-$\sqrt{3}$）∪（$\sqrt{3}$，+∞） | B． | [-$\sqrt{3}$，$\sqrt{3}$] | C． | （-∞，-$\sqrt{3}$]∪[$\sqrt{3}$，+∞） | D． | （-$\sqrt{3}$，$\sqrt{3}$） |
6．已知$\frac{sinα}{1+cosα}$=-$\frac{2}{3}$，则$\frac{sinα}{1-cosα}$的值是（ ）
| A． | $\frac{2}{3}$ | B． | -$\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | -$\frac{3}{2}$ |
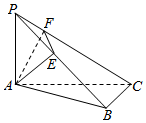如图，P为△ABC所在平面外一点，PA⊥平面ABC，∠ABC=90°，AE⊥PB于E，AF⊥PC于F，求证：