题目内容
15.已知函数$f(x)=\left\{\begin{array}{l}sin(\frac{π}{2}x)-1,x<0\\{log_a}x(a>0,a≠1),x>0\end{array}\right.$的图象上关于y轴对称的点至少有5对,则实数的取值范围是( )| A. | .$(0,\frac{{\sqrt{5}}}{5})$ | B. | $(\frac{{\sqrt{5}}}{5},1)$ | C. | $(0,\frac{1}{3})$ | D. | $(\frac{1}{3},1)$ |
分析 求出函数f(x)=sin($\frac{π}{2}$x)-1,(x<0)关于y轴对称的解析式,利用数形结合即可得到结论.
解答 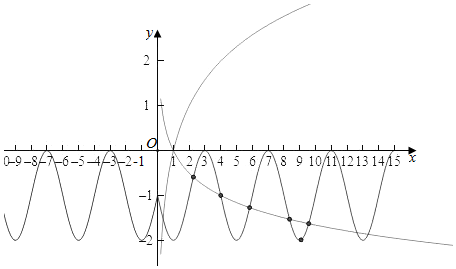 解:若x>0,则-x<0,
解:若x>0,则-x<0,
∵x<0时,f(x)=sin($\frac{π}{2}$x)-1,
∴f(-x)=sin(-$\frac{π}{2}$x)-1=-sin($\frac{π}{2}$x)-1,
则若f(x)=sin($\frac{π}{2}$x)-1,(x<0)关于y轴对称,
则f(-x)=-sin($\frac{π}{2}$x)-1=f(x),
即y=-sin($\frac{π}{2}$x)-1,x>0,
设g(x)=-sin($\frac{π}{2}$x)-1,x>0
作出函数g(x)的图象,
要使y=-sin($\frac{π}{2}$x)-1,x>0与f(x)=logax,x>0的图象至少有5个交点,
则0<a<1且满足f(9)<g(9),
即-2<loga9,
即loga9>logaa-2,
则9<$\frac{1}{{a}^{2}}$,
解得0<a<$\frac{1}{3}$,
故选:C.
点评 本题主要考查分段函数的应用,作出函数关于y轴对称的图象,利用数形结合的思想是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
5.函数f(x)=e2+x-2的零点所在的区间是( )
| A. | (-2,-1) | B. | (-1,0) | C. | (1,2) | D. | (0,1) |
3.已知函数f(x)=x2+sinx,则f′(0)=( )
| A. | 0 | B. | -1 | C. | 1 | D. | 3 |
20.若集合$A=\{x|\frac{2x-3}{x+1}≤1\},B=\{x||x|≤3\}$,则A∩B=( )
| A. | (-1,3] | B. | [-1,3] | C. | [-3,3] | D. | [-3,-1) |
7.下列向量组中,能作为表示它们所在平面内所有向量的基底的是( )
| A. | $\overrightarrow{a}$=(0,0),$\overrightarrow{b}$=(2,3) | B. | $\overrightarrow{a}$=(1,-3),$\overrightarrow{b}$=(2,-6) | C. | $\overrightarrow{a}$=(4,6),$\overrightarrow{b}$=(6,9) | D. | $\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-4,6) |
4. 我国古代数学名著《九章算数》中的更相减损法的思路与如图相似.记R(a\b)为a除以b所得余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出的b的值为( )
我国古代数学名著《九章算数》中的更相减损法的思路与如图相似.记R(a\b)为a除以b所得余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出的b的值为( )
 我国古代数学名著《九章算数》中的更相减损法的思路与如图相似.记R(a\b)为a除以b所得余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出的b的值为( )
我国古代数学名著《九章算数》中的更相减损法的思路与如图相似.记R(a\b)为a除以b所得余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出的b的值为( )| A. | 0 | B. | 1 | C. | 9 | D. | 18 |
5.已知函数f(x)=x3+ax2+x+1存在单调递减区间,则实数α的取值范围为( )
| A. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | B. | [-$\sqrt{3}$,$\sqrt{3}$] | C. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) | D. | (-$\sqrt{3}$,$\sqrt{3}$) |