题目内容
15.(1)已知cosα=-$\frac{4}{5},\;\;α∈(\;π,\;\frac{3π}{2}\;)$,求tanα.(2)若tanα=2,求$\frac{sinα+cosα}{sinα-cosα}$的值.
分析 由条件利用同角三角函数的基本关系,求得所给式子的值.
解答 解:(1)已知cosα=-$\frac{4}{5},\;\;α∈(\;π,\;\frac{3π}{2}\;)$,∴sinα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{3}{5}$,∴tanα=$\frac{sinα}{cosα}$=$\frac{3}{4}$.
(2)若tanα=2,∴$\frac{sinα+cosα}{sinα-cosα}$=$\frac{tanα+1}{tanα-1}$=3.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
相关题目
20.与圆(x-2)2+y2=1相切且在两坐标轴上截距相等的直线共有( )
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 6条 |
7.已知F1,F2是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,过F1的直线与椭圆相交于A,B两点,若∠BAF2=60°,|AB|=|AF2|,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
4.已知|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=2,∠AOB=150°,点C在∠AOB的内部且∠AOC=30°,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,则$\frac{m}{n}$=( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
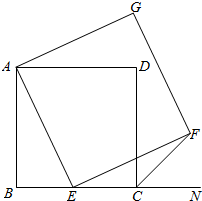 如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.
如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.