题目内容
已知cos2θ=
,其中0<θ<
(1)求tanθ的值
(2)求
的值.
| 7 |
| 25 |
| π |
| 2 |
(1)求tanθ的值
(2)求
2cos2
| ||||
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)已知等式左边利用二倍角的余弦函数公式化简,整理求出cosθ的值,进而求出sinθ的值,即可求出tanθ的值;
(2)原式分子利用二倍角的余弦函数公式化简,分母利用两角和与差的正弦函数公式化简,将各自的值代入计算即可求出值.
(2)原式分子利用二倍角的余弦函数公式化简,分母利用两角和与差的正弦函数公式化简,将各自的值代入计算即可求出值.
解答:
解:(1)∵cos2θ=
,其中0<θ<
,
∴tanθ>0,
由cos2θ=2cos2θ-1=
,得:cos2θ=
,
解得:cosθ=
,sinθ=
,
则tanθ=
;
(2)∵tanθ=
,0<θ<
,
∴cosθ=
=
,sinθ=
=
,
则原式=
=
=
.
| 7 |
| 25 |
| π |
| 2 |
∴tanθ>0,
由cos2θ=2cos2θ-1=
| 7 |
| 25 |
| 16 |
| 25 |
解得:cosθ=
| 4 |
| 5 |
| 3 |
| 5 |
则tanθ=
| 3 |
| 4 |
(2)∵tanθ=
| 3 |
| 4 |
| π |
| 2 |
∴cosθ=
|
| 4 |
| 5 |
| 1-cos2θ |
| 3 |
| 5 |
则原式=
| 1+cosθ-sinθ |
| sinθ+cosθ |
1+
| ||||
|
| 6 |
| 7 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
设i为虚数单位,复数
的共轭复数是( )
| 2i |
| 1-2i |
A、
| ||||
B、-
| ||||
| C、i | ||||
D、-
|
甲乙两人从4门课程中各选修两门,则甲乙所选的课程中至少有1门不相同的选法共有( )种.
| A、30 | B、36 | C、60 | D、72 |
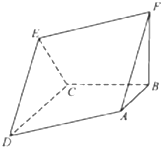 如图所示,四边形ADEF为平行四边形,直线FB⊥平面ABCD,AB∥DC,AB⊥BC,AB=BC=FB=1,CD=2.
如图所示,四边形ADEF为平行四边形,直线FB⊥平面ABCD,AB∥DC,AB⊥BC,AB=BC=FB=1,CD=2.