题目内容
已知p:x2-6x-27≤0,q:|x-1|≤m(m>0),若q是p的必要而不充分条件,则实数m的取值范围是( )
| A、m≤4 | B、m<4 |
| C、m≥8 | D、m>8 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据不等式的性质求出p,q对应的等价条件,利用充分条件和必要条件的定义建立条件关系即可得到结论.
解答:
解:由x2-6x-27≤0,得-3≤x≤9,即p:-3≤x≤9,
由|x-1|≤m(m>0),得1-m≤x≤1+m,即q:1-m≤x≤1+m,
若q是p的必要而不充分条件,
则
,
即
,解得m≥8,
即实数m的取值范围是m≥8,
故选:C
由|x-1|≤m(m>0),得1-m≤x≤1+m,即q:1-m≤x≤1+m,
若q是p的必要而不充分条件,
则
|
即
|
即实数m的取值范围是m≥8,
故选:C
点评:本题主要考查充分条件和必要条件的应用,求出命题的等价条件是解决本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
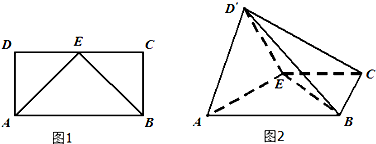
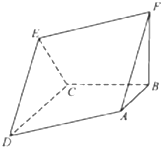 如图所示,四边形ADEF为平行四边形,直线FB⊥平面ABCD,AB∥DC,AB⊥BC,AB=BC=FB=1,CD=2.
如图所示,四边形ADEF为平行四边形,直线FB⊥平面ABCD,AB∥DC,AB⊥BC,AB=BC=FB=1,CD=2.