题目内容
在平面直角坐标系下,曲线C1:
(t为参数),曲线C2:
(θ为参数).若曲线C1,C2有公共点,则实数a的取值范围是 .
|
|
考点:直线的参数方程,圆的参数方程
专题:坐标系和参数方程
分析:第一步:将曲线C1,C2的参数方程均化为普通方程;
第二步:由曲线C1,C2有公共点知,两方程有公共解,联立两方程,消去y或x,得到关于x或y的一元二次方程,由△≥0即可得a的取值范围.
第二步:由曲线C1,C2有公共点知,两方程有公共解,联立两方程,消去y或x,得到关于x或y的一元二次方程,由△≥0即可得a的取值范围.
解答:
解:由
,消去参数t,整理得x=2a-2y,…①
由
及cos2θ+sin2θ=1,消去参数θ,得x2+(y-2)2=4,…②
将①代入②中,消去x并整理得5y2-(8a+4)y+4a2=0,
由于曲线C1,C2有公共点,所以上面关于y的一元二次方程有实数解,
所以△≥0,即(8a+4)2-4×5×4a2≥0,
整理得a2-4a-1≤0,解得2-
≤a≤2+
.
故答案为2-
≤a≤2+
.
|
由
|
将①代入②中,消去x并整理得5y2-(8a+4)y+4a2=0,
由于曲线C1,C2有公共点,所以上面关于y的一元二次方程有实数解,
所以△≥0,即(8a+4)2-4×5×4a2≥0,
整理得a2-4a-1≤0,解得2-
| 5 |
| 5 |
故答案为2-
| 5 |
| 5 |
点评:1.本题也可以利用几何法求解,其思路是:化为普通方程后,由圆心到直线的距离小于或等于圆的半径,解不等式即可.
2.对于两曲线的公共点问题,一般从几何和代数两方面考虑,两种方法各有其优缺点,代数方法具有一般性,但有时计算量比较大;几何方法计算量一般较少,但有时很难找到恰当的式子来表示图形的位置关系,应根据图形的几何特征具体对待.
2.对于两曲线的公共点问题,一般从几何和代数两方面考虑,两种方法各有其优缺点,代数方法具有一般性,但有时计算量比较大;几何方法计算量一般较少,但有时很难找到恰当的式子来表示图形的位置关系,应根据图形的几何特征具体对待.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
sin(π+α)=
,则α角的集合是( )
| 1 |
| 2 |
A、{α|α=2kπ+
| ||||
B、{α|α=2kπ-
| ||||
C、{α|α=2kπ+
| ||||
D、{α|α=2kπ-
|
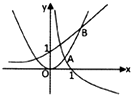 已知y=xa,y=bx,y=logcx中,其中有两个函数具有相反的单调性,另外一个函数是偶函数,如图所示这三个函数部分图象交点A的横坐标是0.65,交点B的横坐标是1.3,则当x∈(0.65,1.3)时,它们的大小关系是( )
已知y=xa,y=bx,y=logcx中,其中有两个函数具有相反的单调性,另外一个函数是偶函数,如图所示这三个函数部分图象交点A的横坐标是0.65,交点B的横坐标是1.3,则当x∈(0.65,1.3)时,它们的大小关系是( )| A、xa>bx>logcx |
| B、bx>logcx>xa |
| C、logcx>xa>bx |
| D、bx>xa>logcx |