题目内容
根据条件分别求出f(x)的解析式:
(1)f(x-2)=2x-
;
(2)f(x2+1)=x4+3x2+4;
(3)f(x)满足f(x)+2f(
)=2x.
(1)f(x-2)=2x-
| x |
(2)f(x2+1)=x4+3x2+4;
(3)f(x)满足f(x)+2f(
| 1 |
| x |
考点:函数解析式的求解及常用方法
专题:方程思想,换元法,函数的性质及应用
分析:(1)利用换元法,设x-2=t,求出x,得出f(t),即得f(x);
(2)利用换元法,设x2+1=t,求出x2,得出f(t),即得f(x);
(3)由f(x)+2f(
)=2x①,得f(
)+2f(x)=
②;从而求出f(x).
(2)利用换元法,设x2+1=t,求出x2,得出f(t),即得f(x);
(3)由f(x)+2f(
| 1 |
| x |
| 1 |
| x |
| 2 |
| x |
解答:
解:(1)∵f(x-2)=2x-
,
设x-2=t,∴x=t+2(t≥-2);
∴f(t)=2(t+2)-
,
即f(x)=2(x+2)-
(x≥-2);
(2)∵f(x2+1)=x4+3x2+4,
设x2+1=t,∴x2=t-1(t≥1);
∴f(t)=(t-1)2+3(t-1)+4=t2+t+2,
即f(x)=x2+x+2(x≥1);
(3)∵f(x)满足f(x)+2f(
)=2x①,
∴f(
)+2f(x)=
②;
②×2-①得,3f(x)=
-2x,
∴f(x)=
-
.
| x |
设x-2=t,∴x=t+2(t≥-2);
∴f(t)=2(t+2)-
| t+2 |
即f(x)=2(x+2)-
| x+2 |
(2)∵f(x2+1)=x4+3x2+4,
设x2+1=t,∴x2=t-1(t≥1);
∴f(t)=(t-1)2+3(t-1)+4=t2+t+2,
即f(x)=x2+x+2(x≥1);
(3)∵f(x)满足f(x)+2f(
| 1 |
| x |
∴f(
| 1 |
| x |
| 2 |
| x |
②×2-①得,3f(x)=
| 4 |
| x |
∴f(x)=
| 4 |
| 3x |
| 2x |
| 3 |
点评:本题考查了求函数解析式的问题,也考查了方程思想与换元法的应用问题,是基础题.

练习册系列答案
相关题目
满足sinx≥
的x的集合为( )
| 1 |
| 2 |
A、{x|2kπ+
| ||||
B、{x|2kπ+
| ||||
C、{x|2kπ-
| ||||
D、{x|2kπ-
|
已知数列:1,a+a2,a2+a3+a4,a3+a4+a5+a6,…,则数列的第k项为( )
| A、ak+ak+1+…+a2k |
| B、ak-1+ak+…+a2k-1 |
| C、ak-1+ak+…+a2k |
| D、ak-1+ak+…+a2k-2 |
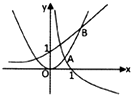 已知y=xa,y=bx,y=logcx中,其中有两个函数具有相反的单调性,另外一个函数是偶函数,如图所示这三个函数部分图象交点A的横坐标是0.65,交点B的横坐标是1.3,则当x∈(0.65,1.3)时,它们的大小关系是( )
已知y=xa,y=bx,y=logcx中,其中有两个函数具有相反的单调性,另外一个函数是偶函数,如图所示这三个函数部分图象交点A的横坐标是0.65,交点B的横坐标是1.3,则当x∈(0.65,1.3)时,它们的大小关系是( )| A、xa>bx>logcx |
| B、bx>logcx>xa |
| C、logcx>xa>bx |
| D、bx>xa>logcx |
已知A、B、C、D为同一球面上的四点,且连接每点间的线段长都等于2,则球心O到平面BCD的距离等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|