题目内容
若某几何体的三视图 (单位:cm) 如图所示,则此几何体的体积是( )cm3


| A、π | B、2π | C、3π | D、4π |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:此几何体为圆锥的一半,即可得出.
解答:
解:由三视图可知:此几何体为圆锥的一半,
∴此几何体的体积=
×
×π×22×3=2π.
故选:B.
∴此几何体的体积=
| 1 |
| 2 |
| 1 |
| 3 |
故选:B.
点评:本题考查了由三视图恢复原几何体的体积计算,属于基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知函数y=f(x)的图象在区间[a,b]上是连续不断的,且满足f(a)•f(b)<0(a,b∈R,a<b),则函数f(x)在(a,b)内( )
| A、无零点 |
| B、有且只有一个零点 |
| C、至少有一个零点 |
| D、无法确定有无零点 |
函数f(x)=lgx+x的零点所在的区间为( )
A、(
| ||||
B、(0,
| ||||
C、(
| ||||
| D、(1,2) |
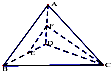 如图,在三棱锥A-BCD中,BC=CD=DB,AB=AC=AD;E,F为棱BD,AD的中点,若EF⊥CF,则直线BD与平面ACD所成的角为
如图,在三棱锥A-BCD中,BC=CD=DB,AB=AC=AD;E,F为棱BD,AD的中点,若EF⊥CF,则直线BD与平面ACD所成的角为