题目内容
将4名实习教师分配到高一年级三个班实习，每班至少安排一名教师，则不同的分配方案有（ ）种．
| A、12 | B、36 | C、72 | D、108 |
考点：计数原理的应用
专题：排列组合
分析：根据分步计数原理，合理的进行分步，把其中的2名教师看做一个元素，然后进行全排列，问题即可解得．
解答：
解：第一步从4名实习教师中选出2名组成一个复合元素，共有
=6种，
第二步把3个元素（包含一个复合元素）安排到三个班实习有
=6种，
根据分步计数原理不同的分配方案有6×6=36种．
故选：B．
| C | 2 4 |
第二步把3个元素（包含一个复合元素）安排到三个班实习有
| A | 3 3 |
根据分步计数原理不同的分配方案有6×6=36种．
故选：B．
点评：本题主要考查了分步计数原理，解决排列组合的混合问题，先选后排是基本的指导思想．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
某商品销售量y（件）与销售价格x（元/件）负相关，则其回归方程可能是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
经过点（1，1）作曲线 y=x3的切线的方程为（ ）
| A、3x-y-2=0 |
| B、x-y=0 |
| C、3x-y-2=0或3x-4y+l=0 |
| D、3x-y-2=0或x-y=0 |
给出下列四个函数图象和函数的四个关系式：
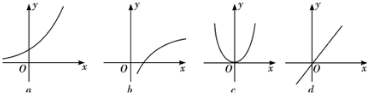
①f（x+y）=f（x）+f（y）；
②g（x+y）=g（x）•g（y）；
③u（x•y）=u（x）+u（y）；
④v（x•y）=v（x）•v（y），已知每个函数图象都有满足其中的一个关系式，则它们之间的对应是（ ）
①f（x+y）=f（x）+f（y）；
②g（x+y）=g（x）•g（y）；
③u（x•y）=u（x）+u（y）；
④v（x•y）=v（x）•v（y），已知每个函数图象都有满足其中的一个关系式，则它们之间的对应是（ ）
| A、①→a ②→d ③→c ④→b |
| B、①→b ②→c ③→a ④→d |
| C、①→c ②→a ③→b ④→d |
| D、①→d ②→a ③→b ④→c |
AB是半径为1的圆的直径，在AB上的任意一点M，过点M垂直于AB的弦，则弦长大于
的概率是（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若复数（1+i）（1+ai）（a∈R，i是虚数单位）是纯虚数，则a=（ ）
| A、1 | B、-1 | C、0 | D、2 |
记直线x-3y-l=0的倾斜角为α，曲线y=1nx在（2，1n2）处切线的倾斜角为β，则α+β=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
135°化成弧度为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
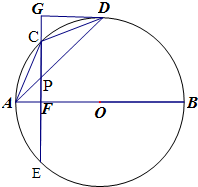如图，AB为⊙O的直径，点D是⊙O上的一点，点C是弧AD的中点，弦CE⊥AB于F．GD是⊙O的切线，且与EC的延长线相交于点G，连接AD，交CE于点P．