题目内容
已知等比数列{an}满足a3-a2=10,a1a2a3=125.
(Ⅰ)求数列an的前n项和Sn;
(Ⅱ)设bn=n(Sn+
),Tn=b1+b2+b3+…+bn,求Tn.
(Ⅰ)求数列an的前n项和Sn;
(Ⅱ)设bn=n(Sn+
| 5 |
| 6 |
考点:数列的求和,等比数列的前n项和
专题:计算题,等差数列与等比数列
分析:(Ⅰ)设等比数列{an}的公比为q,由a1a2a3=125.可得a2=5,又a3-a2=10,a3=15求出首项与公比及前n项和.
(Ⅱ)由(Ⅰ)知,bn=n(Sn+
)=n[
(3n-1)+
]=
n•3n利用错位相减求出前n项和.
(Ⅱ)由(Ⅰ)知,bn=n(Sn+
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 6 |
解答:
解:(Ⅰ)设等比数列{an}的公比为q,由a1a2a3=125.
可得a2=5,又a3-a2=10,
∴a3=15
∴q=
=3
∴a1=
=
∴Sn=
=
(3n-1)
(Ⅱ)由(Ⅰ)知,bn=n(Sn+
)=n[
(3n-1)+
]=
n•3n
∴Tn=
(1×3+2×32+…+n•3n)
设An=1×3+2×32+…+n•3n①
3An= 1×32+…+(n-1)•3n + n•3n+1②
②-①得2An=-3-32-33-…-3n+n•3n+1
=-
+n•3n+1
∴An=-
×
+
•3n+1
=
•3n+1+
∴Tn=
An=
•3n+
可得a2=5,又a3-a2=10,
∴a3=15
∴q=
| a3 |
| a2 |
∴a1=
| a2 |
| q |
| 5 |
| 3 |
∴Sn=
| ||
| 1-3 |
| 5 |
| 6 |
(Ⅱ)由(Ⅰ)知,bn=n(Sn+
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 6 |
∴Tn=
| 5 |
| 6 |
设An=1×3+2×32+…+n•3n①
3An= 1×32+…+(n-1)•3n + n•3n+1②
②-①得2An=-3-32-33-…-3n+n•3n+1
=-
| 3-3n+1 |
| 1-3 |
∴An=-
| 1 |
| 2 |
| 3-3n+1 |
| 1-3 |
| n |
| 2 |
=
| 2n-1 |
| 4 |
| 3 |
| 4 |
∴Tn=
| 5 |
| 6 |
| 10n-5 |
| 8 |
| 5 |
| 8 |
点评:本题考查数列通项公式及前n项和的求法,求和的关键是先求通项,据通项特点选择合适的方法,属于一道中档题.

练习册系列答案
相关题目
给出下列四个函数图象和函数的四个关系式:
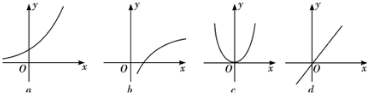
①f(x+y)=f(x)+f(y);
②g(x+y)=g(x)•g(y);
③u(x•y)=u(x)+u(y);
④v(x•y)=v(x)•v(y),已知每个函数图象都有满足其中的一个关系式,则它们之间的对应是( )

①f(x+y)=f(x)+f(y);
②g(x+y)=g(x)•g(y);
③u(x•y)=u(x)+u(y);
④v(x•y)=v(x)•v(y),已知每个函数图象都有满足其中的一个关系式,则它们之间的对应是( )
| A、①→a ②→d ③→c ④→b |
| B、①→b ②→c ③→a ④→d |
| C、①→c ②→a ③→b ④→d |
| D、①→d ②→a ③→b ④→c |
135°化成弧度为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
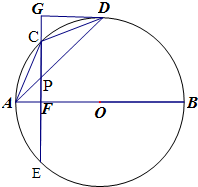 如图,AB为⊙O的直径,点D是⊙O上的一点,点C是弧AD的中点,弦CE⊥AB于F.GD是⊙O的切线,且与EC的延长线相交于点G,连接AD,交CE于点P.
如图,AB为⊙O的直径,点D是⊙O上的一点,点C是弧AD的中点,弦CE⊥AB于F.GD是⊙O的切线,且与EC的延长线相交于点G,连接AD,交CE于点P.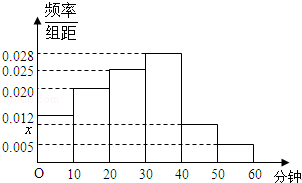 漳州三中高三年为了了解高三理科学生对数学学科的兴趣情况,随机抽取了高三年100名理科同学进行调查,如图是根据调查结果绘制的晚自习第一节课学习数学时间的频率分布直方图,其中学习数学学科的时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].将学习时间不低于40分钟的同学称为“数学迷”.
漳州三中高三年为了了解高三理科学生对数学学科的兴趣情况,随机抽取了高三年100名理科同学进行调查,如图是根据调查结果绘制的晚自习第一节课学习数学时间的频率分布直方图,其中学习数学学科的时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].将学习时间不低于40分钟的同学称为“数学迷”.