题目内容
在数列{an}中，它的前n项和为Sn=an2+bn+3a-2（n∈N*，其中a，b是常数），若数列{an}是等差数列，则它的公差是（ ）
A、
| ||
| B、1 | ||
C、
| ||
| D、与a有关 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：利用等差数列的性质即可得出．
解答：
解：∵数列{an}是等差数列，前n项和为Sn=an2+bn+3a-2，
∴3a-2=0，解得a=
．
∴Sn=
n2+bn，
∴d=S2-2S1
=
×22+2b-2[
×12+b×1]
=
．
故选：A．
∴3a-2=0，解得a=
| 2 |
| 3 |
∴Sn=
| 2 |
| 3 |
∴d=S2-2S1
=
| 2 |
| 3 |
| 2 |
| 3 |
=
| 4 |
| 3 |
故选：A．
点评：本题考查了等差数列的性质，属于中档题．
练习册系列答案
相关题目
终边在直线y=x上的角的集合为（ ）
A、{α|α=kπ+
| ||
B、{α|α=kπ+
| ||
C、{α|α=2kπ+
| ||
D、{α|α=2kπ+
|
经过点（1，1）作曲线 y=x3的切线的方程为（ ）
| A、3x-y-2=0 |
| B、x-y=0 |
| C、3x-y-2=0或3x-4y+l=0 |
| D、3x-y-2=0或x-y=0 |
已知tanα=-
，则
=（ ）
| 1 |
| 2 |
| (cosα-sinα)2 |
| cos2α |
| A、2 | B、-2 | C、3 | D、-3 |
给出下列四个函数图象和函数的四个关系式：
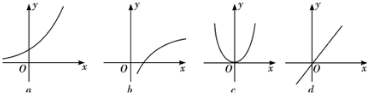
①f（x+y）=f（x）+f（y）；
②g（x+y）=g（x）•g（y）；
③u（x•y）=u（x）+u（y）；
④v（x•y）=v（x）•v（y），已知每个函数图象都有满足其中的一个关系式，则它们之间的对应是（ ）
①f（x+y）=f（x）+f（y）；
②g（x+y）=g（x）•g（y）；
③u（x•y）=u（x）+u（y）；
④v（x•y）=v（x）•v（y），已知每个函数图象都有满足其中的一个关系式，则它们之间的对应是（ ）
| A、①→a ②→d ③→c ④→b |
| B、①→b ②→c ③→a ④→d |
| C、①→c ②→a ③→b ④→d |
| D、①→d ②→a ③→b ④→c |
AB是半径为1的圆的直径，在AB上的任意一点M，过点M垂直于AB的弦，则弦长大于
的概率是（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
记直线x-3y-l=0的倾斜角为α，曲线y=1nx在（2，1n2）处切线的倾斜角为β，则α+β=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|