题目内容

用秦九韶算法求多项式f（x）=7x6+6x4+3x2+2当x=4时的值时，先算的是（　　）
A、4×4=16
B、4×4×4×4×4×4=4096
C、7×4+6=34
D、7×4+0=28
考点：中国古代数学瑰宝
专题：算法和程序框图
分析：用秦九韶算法求多项式f（x）=（（（（（7x+0）x+6）x+0）x+3）x+0）x+2，即可得出．
解答： 解：用秦九韶算法求多项式f（x）=7x6+6x4+3x2+2=（（（（（7x+0）x+6）x+0）x+3）x+0）x+2，
当x=4时的值时，先算的是7×4+0=28．
故选：D．
点评：本题考查了利用秦九韶算法求多项式的值，属于基础题．
练习册系列答案
相关题目
求过两点A（0，4），B（4，6）且圆心在直线x-2y-2=0上的圆的标准方程
 
．
命题“?x＞1，x2≥3”的否定是
 
．
已知函数f（x）=
1
3
x3-ax2-3a2x，其中a≥0
（1）若f′（0）=-3，求a的值；
（2）在（1）条件下，求曲线y=f（x）在点（1，f（1））处的切线方程；
（3）求函数f（x）在区间[0，2]上的最小值．
函数f（x）=2sin（ωx+
π
3
），又f（α）=-2，f（β）=0，且|α-β|的最小值为
π
2
，则正数ω=
 
．
设α，β都是锐角，且sinα=
10
10
，sinβ=
5
5
，则α+β=（　　）
A、
π
4
B、
π
2
C、
3π
4
D、
π
4
或
3π
4
某商品销售量y（件）与销售价格x（元/件）负相关，则其回归方程可能是（　　）
A、
y
=5x-10
B、
y
=5x+10
C、
y
=-5x-10
D、
y
=-5x+10
函数y=
cosx
1-sin2x
+
sinx
1-cos2x
+
tanx
tan2x
的值域是（　　）
A、{3，-1}
B、{1，3}
C、{-3，-1，1}
D、{-1，1，3}
给出下列四个函数图象和函数的四个关系式：

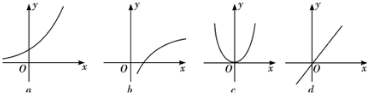
①f（x+y）=f（x）+f（y）；
②g（x+y）=g（x）•g（y）；
③u（x•y）=u（x）+u（y）；
④v（x•y）=v（x）•v（y），已知每个函数图象都有满足其中的一个关系式，则它们之间的对应是（　　）
A、①→a ②→d ③→c ④→b
B、①→b ②→c ③→a ④→d
C、①→c ②→a ③→b ④→d
D、①→d ②→a ③→b ④→c

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网