题目内容
a=cos50°cos127°+cos40°cos37°,b=
(sin56°-cos56°),c=
,d=
(cos80°-2cos250°+1),则a,b,c,d的大小关系为( )
| ||
| 2 |
| 1-tan239° |
| 1+tan239° |
| 1 |
| 2 |
| A、a>b>d>c |
| B、b>a>d>c |
| C、a>c>b>d |
| D、c>a>b>d |
考点:两角和与差的正弦函数
专题:三角函数的求值,三角函数的图像与性质
分析:利用两角和公式和倍角公式对a,b,c,d分别化简,利用诱导公式再转化成单调区间的正弦函数,最后理由正弦函数的单调性求得答案.
解答:
解:a=sin40°cos127°+cos40°sin127°=sin(40°+127°)=sin167°=sin13,
b=
(sin56°-cos56°)=
sin56°-
cos56°=sin(56°-45°)=sin11°
c=
=cos239°-sin239°=cos78°=sin12°,
d=
cos80°-
cos100°=
cos80°+
cos80°=cos80°=sin10°
∵sin10°<sin11°<sin12°<sin13,
∴d<b<c<a.
故选:C.
b=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
c=
| cos239°-sin239° | ||||
|
d=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵sin10°<sin11°<sin12°<sin13,
∴d<b<c<a.
故选:C.
点评:本题主要考查了两角和公式,二倍角角公式,诱导公式的应用,正弦函数的单调性.为了便于比较,应把每一项转化成同名函数,且在一个单调区间.

练习册系列答案
相关题目
函数y=
+
+
的值域是( )
| cosx | ||
|
| sinx | ||
|
| tanx | ||
|
| A、{3,-1} |
| B、{1,3} |
| C、{-3,-1,1} |
| D、{-1,1,3} |
给出下列四个函数图象和函数的四个关系式:
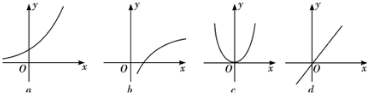
①f(x+y)=f(x)+f(y);
②g(x+y)=g(x)•g(y);
③u(x•y)=u(x)+u(y);
④v(x•y)=v(x)•v(y),已知每个函数图象都有满足其中的一个关系式,则它们之间的对应是( )

①f(x+y)=f(x)+f(y);
②g(x+y)=g(x)•g(y);
③u(x•y)=u(x)+u(y);
④v(x•y)=v(x)•v(y),已知每个函数图象都有满足其中的一个关系式,则它们之间的对应是( )
| A、①→a ②→d ③→c ④→b |
| B、①→b ②→c ③→a ④→d |
| C、①→c ②→a ③→b ④→d |
| D、①→d ②→a ③→b ④→c |
若复数(1+i)(1+ai)(a∈R,i是虚数单位)是纯虚数,则a=( )
| A、1 | B、-1 | C、0 | D、2 |
记直线x-3y-l=0的倾斜角为α,曲线y=1nx在(2,1n2)处切线的倾斜角为β,则α+β=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知全集U=R,集合A={x|
<0},B={y|y=2x,x≥0},则集合{x|x≤0}=( )
| x-1 |
| x |
| A、A∩B |
| B、A∪B |
| C、CU(A∩B) |
| D、CU(A∪B) |
135°化成弧度为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
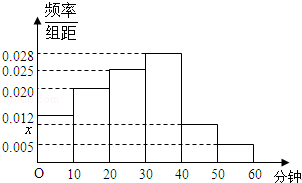 漳州三中高三年为了了解高三理科学生对数学学科的兴趣情况,随机抽取了高三年100名理科同学进行调查,如图是根据调查结果绘制的晚自习第一节课学习数学时间的频率分布直方图,其中学习数学学科的时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].将学习时间不低于40分钟的同学称为“数学迷”.
漳州三中高三年为了了解高三理科学生对数学学科的兴趣情况,随机抽取了高三年100名理科同学进行调查,如图是根据调查结果绘制的晚自习第一节课学习数学时间的频率分布直方图,其中学习数学学科的时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].将学习时间不低于40分钟的同学称为“数学迷”.