题目内容
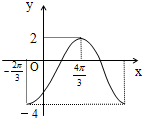 已知函数y=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ)+B(A>0,ω>0,|φ|<| π |
| 2 |
(1)求函数的解析式;
(2)若函数g(x)=f(mx)+1(m>0)的图象关于点M(
| 4π |
| 3 |
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:综合题,三角函数的图像与性质
分析:(1)根据最值求出A,B,利用周期求出ω,结合最大值求出φ,可得函数的解析式;
(2)利用对称性,求出m=
k+
,k∈N,结合函数在区间[0,
]上不是单调函数,求m的取值所构成的集合.
(2)利用对称性,求出m=
| 3 |
| 2 |
| 1 |
| 4 |
| π |
| 2 |
解答:
解:(1)由图象得T=4π,∴ω=
,
又A>0,∴
解得A=3,B=-1…(3分)
∴y=3sin(
x+φ)-1
∵f(
)=2,∴sin(
+φ)=1,
∵|φ|<
,
∴φ=-
,
∴y=3sin(
x-
)-1…(5分)
(2)g(x)=f(mx)+1=3sin(
x-
),
∵函数g(x)=f(mx)+1(m>0)的图象关于点M(
,0)对称,
∴g(
+x)=-g(
-x),
令x=0,则g(
)=0,
∴3sin(
-
)=0,
∴
-
=kπ,
∴m=
k+
,k∈N…(8分)
k=0,m=
;k=1,m=
,函数在区间[0,
]上单调递增,
k≥2,m≥
,函数在区间[0,
]上不是单调函数,
综上,m的取值所构成的集合为{m|m=
k+
,k∈N且k≥2}.…(12分)
| 1 |
| 2 |
又A>0,∴
|
解得A=3,B=-1…(3分)
∴y=3sin(
| 1 |
| 2 |
∵f(
| 4π |
| 3 |
| 2π |
| 3 |
∵|φ|<
| π |
| 2 |
∴φ=-
| π |
| 6 |
∴y=3sin(
| 1 |
| 2 |
| π |
| 6 |
(2)g(x)=f(mx)+1=3sin(
| m |
| 2 |
| π |
| 6 |
∵函数g(x)=f(mx)+1(m>0)的图象关于点M(
| 4π |
| 3 |
∴g(
| 4π |
| 3 |
| 4π |
| 3 |
令x=0,则g(
| 4π |
| 3 |
∴3sin(
| 2mπ |
| 3 |
| π |
| 6 |
∴
| 2mπ |
| 3 |
| π |
| 6 |
∴m=
| 3 |
| 2 |
| 1 |
| 4 |
k=0,m=
| 1 |
| 4 |
| 7 |
| 4 |
| π |
| 2 |
k≥2,m≥
| 13 |
| 4 |
| π |
| 2 |
综上,m的取值所构成的集合为{m|m=
| 3 |
| 2 |
| 1 |
| 4 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求函数的解析式,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
用反证法证明命题:若p则q.其第一步是反设命题的结论不成立,这个正确的反设是( )
| A、若p,则¬q | B、若¬p,则q |
| C、¬p | D、¬q |
若F1,F2是椭圆
+
=1的两个焦点,A、B是过焦点F1的弦,则△ABF2的周长为( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、6 | B、4 | C、12 | D、8 |
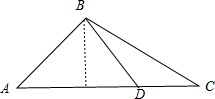 如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积.
如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积. 在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=2,E是BC的中点,建立空间直角坐标系,用向量方法解决下列问题.
在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=2,E是BC的中点,建立空间直角坐标系,用向量方法解决下列问题.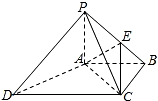 四棱锥P-ABCD中,DC∥AB,AB=2DC=4
四棱锥P-ABCD中,DC∥AB,AB=2DC=4