题目内容
若F1，F2是椭圆
+
=1的两个焦点，A、B是过焦点F1的弦，则△ABF2的周长为（ ）
| x2 |
| 9 |
| y2 |
| 4 |
| A、6 | B、4 | C、12 | D、8 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出椭圆的a=3，由椭圆的定义，可得△ABF2的周长为4a，计算即可得到．
解答：
解：椭圆
+
=1的a=3，
由椭圆的定义，可得，
|AF1|+|AF2|=|BF1|+|BF2|=2a，
则△ABF2的周长为|AB|+|AF2|+|BF2|
=|AF1|+|BF1|+|AF2|+|BF2|=4a=12．
故选C．
| x2 |
| 9 |
| y2 |
| 4 |
由椭圆的定义，可得，
|AF1|+|AF2|=|BF1|+|BF2|=2a，
则△ABF2的周长为|AB|+|AF2|+|BF2|
=|AF1|+|BF1|+|AF2|+|BF2|=4a=12．
故选C．
点评：本题考查椭圆的方程和性质，主要考查椭圆的定义，考查运算能力，属于基础题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
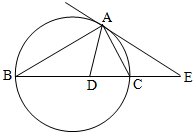如图，△ABC的外接圆的切线AE与BC的延长线交于点E，∠BAC的平分线与BC交于点D．
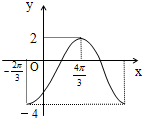已知函数y=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜