题目内容
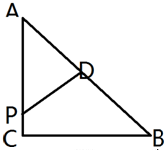如图已知△ABC，∠C=90°，|| CA |
| CB |
| DP |
| BC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：只需要考虑向量
在向量
的投影即可，而投影长始终为1，而向量
和向量
的夹角为锐角，问题得以解决．
| DP |
| BC |
| DP |
| BC |
解答：
解：如图，过点D作DE⊥BC，垂足为E，
∵D是AB中点，∠C=90°，|
|=|
|=2，
∴|
|=
|
|=1
∵向量
为
在向量
的投影，
∴投影长始终为1，
∵向量
和向量
的夹角为锐角，
∴
•
=|
|•1=2，
故答案为：2
解：如图，过点D作DE⊥BC，垂足为E，∵D是AB中点，∠C=90°，|
| CA |
| CB |
∴|
| EC |
| 1 |
| 2 |
| BC |
∵向量
| EC |
| DP |
| BC |
∴投影长始终为1，
∵向量
| DP |
| BC |
∴
| DP |
| BC |
| BC |
故答案为：2
点评：本题主要考查了向量的数量积的运算，关键是理解向量
在向量
的投影长不变，属于中档题．
| DP |
| BC |
练习册系列答案
黎明文化寒假作业系列答案
相关题目
下列说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题是“若x2=1，则x≠1” | ||
| B、“x=-1”是“x2-x-2=0”的必要不充分条件 | ||
C、“tanx=1”是“x=
| ||
| D、命题“若x=y，则sinx=siny”的逆否命题是真命题 |
下列命题中是假命题的是（ ）
| A、?a，b∈R+，lg（a+b）≠lga+lgb |
| B、?φ∈R，函数f（x）=sin（2x+φ）是偶函数 |
| C、?α，β∈R，使得cos（α+β）=cosα+cosβ |
| D、?m∈R，使f（x）=（m-1）•xm2-4m+3是幂函数，且在（0，+∞）上递减 |
命题“?x∈[-∞，0），x3+x≥0”的否定是（ ）
| A、?x∈[-∞，0），x3+x＜0 |
| B、?x∈（-∞，0），x3+x≥0 |
| C、?x0∈[0，+∞），x03+x0＜0 |
| D、?x0∈[0，+∞），x03+x0≥0 |
设集合A={x|x2-1＜0}，B={x|y=
}，则A∩B等于（ ）
log
|
| A、{x|x＞1} |
| B、{x|0＜x＜1} |
| C、{x|x＜1} |
| D、{x|0＜x≤1} |