题目内容
已知f（x）=-x2，g（x）=2x-m，若对任意x1∈[-1，3]，总存在x2∈[0，2]，使f（x1）≥g（x2）成立，则实数m的取值范围是 ．
考点：函数恒成立问题
专题：函数的性质及应用
分析：条件对任意x1∈[-1，3]，总存在x2∈[0，2]，使f（x1）≥g（x2）成立等价为上f（x）min≥g（x）min即可．
解答：
解：∵x1∈[-1，3]，∴-9≤f（x1）≤0，
∵x2∈[0，2]，∴1-m≤g（x2）≤4-m，
若对任意x1∈[-1，3]，总存在x2∈[0，2]，使f（x1）≥g（x2）成立，
则f（x）min≥g（x）min即可，
即-9≥1-m，
解得m≥10，
故答案为：[10，+∞）
∵x2∈[0，2]，∴1-m≤g（x2）≤4-m，
若对任意x1∈[-1，3]，总存在x2∈[0，2]，使f（x1）≥g（x2）成立，
则f（x）min≥g（x）min即可，
即-9≥1-m，
解得m≥10，
故答案为：[10，+∞）
点评：本题主要考查函数值的大小比较以及不等式恒成立问题，将条件转化为求函数最值之间的关系是解决本题的关键．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
数列1，-3，5，-7，9，…的一个通项公式{an}=（ ）
| A、2n-1 |
| B、（-1）n（2n+1） |
| C、（-1）n（2n-1） |
| D、（-1）n+1（2n-1） |
设f（x）为奇函数，且在（-∞，0）内是减函数，f（3）=0，则x f（x）＜0的解集为（ ）
| A、（-3，0）∪（3，+∞） |
| B、（-∞，-3）∪（0，3 ） |
| C、（-3，0）∪（0，3 ） |
| D、（-∞，-3）∪（3，+∞） |
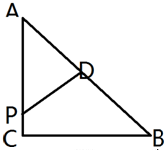如图已知△ABC，∠C=90°，|