题目内容
已知f(x)=
是定义在(-1,1)上的函数.
(1)证明f(-x)=-f(x);
(2)利用函数单调性的定义证明:f(x)是定义域上的增函数.
| x |
| 1+x2 |
(1)证明f(-x)=-f(x);
(2)利用函数单调性的定义证明:f(x)是定义域上的增函数.
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)求f(-x)即可得到f(-x)=-f(x);
(2)设x1,x2∈(-1,1),且x1<x2,根据单调性的定义证明f(x1)<f(x2)即可.
(2)设x1,x2∈(-1,1),且x1<x2,根据单调性的定义证明f(x1)<f(x2)即可.
解答:
证:(1)f(-x)=
=-f(x),即f(-x)=-f(x);
(2)设-1<x1<x2<1,则:
f(x1)-f(x2)=
-
=
;
∵-1<x1<x2<1,∴x2-x1>0,x1x2-1<0;
∴f(x1)<f(x2);
∴f(x)是(-1,1)上的增函数.
| -x |
| 1+x2 |
(2)设-1<x1<x2<1,则:
f(x1)-f(x2)=
| x1 |
| 1+x12 |
| x2 |
| 1+x22 |
| (x2-x1)(x1x2-1) |
| (1+x12)(1+x22) |
∵-1<x1<x2<1,∴x2-x1>0,x1x2-1<0;
∴f(x1)<f(x2);
∴f(x)是(-1,1)上的增函数.
点评:考查函数单调性的定义,以及根据单调性的定义证明函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
四面体S-ABC中,已知SA⊥AB,AB⊥BC,|
|=3,|
|=4,|
|=5,|
|=
,则二面角S-AB-C的大小为( )
| SA |
| AB |
| BC |
| SC |
| 35 |
A、
| ||
B、
| ||
C、
| ||
D、
|
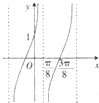 已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<
已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、kπ+
| ||||
D、
|
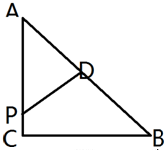 如图已知△ABC,∠C=90°,|
如图已知△ABC,∠C=90°,|