题目内容
已知函数f(x)=-x2-4x-3,若
(1)x∈R,求值域;
(2)x∈[-2,0],求值域;
(3)x∈[-2,3],求值域.
(1)x∈R,求值域;
(2)x∈[-2,0],求值域;
(3)x∈[-2,3],求值域.
考点:二次函数的性质,二次函数在闭区间上的最值
专题:函数的性质及应用
分析:(1)(2)(3)先求出函数的单调区间,从而求出函数的值域.
解答:
解:(1)∵f(x)=-x2-4x-3=-(x+2)2+1,
∴f(x)max=f(-2)=1,
∴函数f(x)的值域是:(-∞,1];
(2)由(1)得:f(x)在[-2,0]递减,
∴f(x)min=f(0)=-3,f(x)max=f(-2)=1,
∴x∈[-2,0]时,f(x)∈[-3,1];
(3)由(1)得:f(x)在[-2,3]递减,
∴f(x)min=f(3)=-24,f(x)max=f(-2)=1,
∴x∈[-2,3]时,f(x)∈[-24,1];
∴f(x)max=f(-2)=1,
∴函数f(x)的值域是:(-∞,1];
(2)由(1)得:f(x)在[-2,0]递减,
∴f(x)min=f(0)=-3,f(x)max=f(-2)=1,
∴x∈[-2,0]时,f(x)∈[-3,1];
(3)由(1)得:f(x)在[-2,3]递减,
∴f(x)min=f(3)=-24,f(x)max=f(-2)=1,
∴x∈[-2,3]时,f(x)∈[-24,1];
点评:本题考查了二次函数的性质,考查函数的单调性,函数的最值问题,是一道基础题.

练习册系列答案
相关题目
数列1,-3,5,-7,9,…的一个通项公式{an}=( )
| A、2n-1 |
| B、(-1)n(2n+1) |
| C、(-1)n(2n-1) |
| D、(-1)n+1(2n-1) |
计算:i(i+1)=( )
| A、i+1 | B、i-1 |
| C、-i+1 | D、-i-1 |
已知复数z满足(1-i)z=2,则z=( )
| A、-1-i | B、-1+i |
| C、1-i | D、1+i |
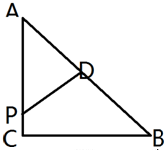 如图已知△ABC,∠C=90°,|
如图已知△ABC,∠C=90°,|