Question

15．已知不等式组$\left\{\begin{array}{l}{y≤5}&{\;}\\{2x-y+3≤0}&{\;}\\{x+y-1≥0}&{\;}\end{array}\right.$表示的平面区域为D，若?（x，y）∈D，|x|+2y≤a为真命题，则实数a的取值范围是（　　）

• A． [10，+∞）
• B． [11，+∞）
• C． [13，+∞）
• D． [14，+∞）

Answer 1

分析 画出约束条件的可行域，求出|x|+2y的最大值，即可得到?（x，y）∈D，|x|+2y≤a为真命题，实数a的取值范围．

解答 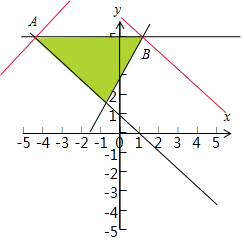解：不等式组$\left\{\begin{array}{l}{y≤5}&{\;}\\{2x-y+3≤0}&{\;}\\{x+y-1≥0}&{\;}\end{array}\right.$表示的平面区域为D，如图：
当x≥0时，z=|x|+2y=x+2y，z=x+2y经过B时取得最大值，
由$\left\{\begin{array}{l}{y=5}\\{2x-y+3=0}\end{array}\right.$可得B（1，5），此时z的最大值为：11．
当x＜0时，z=|x|+2y=-x+2y，z=-x+2y经过A时取得最大值，
由$\left\{\begin{array}{l}{y=5}\\{x+y-1=0}\end{array}\right.$，可得A（-4，5），此时z的最大值为：
14．
若?（x，y）∈D，|x|+2y≤a为真命题，则实数a的取值范围：[14，+∞）．
故选：D．

点评 本题考查命题的真假的判断与应用，线性规划的简单应用，考查转化思想以及数形结合思想的应用．