题目内容
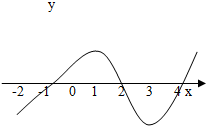 如图是函数y=f(x)的导函数f′(x)的图象,对下列四个判断:
如图是函数y=f(x)的导函数f′(x)的图象,对下列四个判断:①y=f(x)在(-2,-1)上是增函数;
②x=-1是极小值点;
③f(x)在(-1,2)上是增函数,在(2,4)上是减函数;
④x=3是f(x)的极小值点;
其中正确的是( )
| A、①② | B、③④ | C、②③ | D、②④ |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:通过导函数的图象,判断出函数的单调区间,函数的极值,从而得出答案.
解答:
解:对于①:在区间(-2,-1)上,f′(x)<0,f(x)是减函数,故①错误;
对于②:在区间(-2,-1)上,f′(x)<0,f(x)递减,
区间(-1,2)上,f′x)>0,f(x)递增,∴x=-1是极小值点,故②正确;
对于③:在区间(-1,2)上,f′(x)>0,f(x)是增函数,
在(2,4)上,f′(x)<0,f(x)是减函数,故③正确;
对于④:f(-3)<0,故④错误;
故选:C.
对于②:在区间(-2,-1)上,f′(x)<0,f(x)递减,
区间(-1,2)上,f′x)>0,f(x)递增,∴x=-1是极小值点,故②正确;
对于③:在区间(-1,2)上,f′(x)>0,f(x)是增函数,
在(2,4)上,f′(x)<0,f(x)是减函数,故③正确;
对于④:f(-3)<0,故④错误;
故选:C.
点评:本题考查了函数的单调性,函数的极值问题,考查数形结合思想,是一道基础题.

练习册系列答案
相关题目
袋子中有3个红球和2个黑球,从中摸出一个球,该球为黑球的概率是( )
A、
| ||
| B、1 | ||
C、
| ||
D、
|
若α∈(0,
),且sin2α+cos2α=
,则tanα的值等于( )
| π |
| 2 |
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若函数f(x)是定义在[-6,6]的偶函数,且在[-6,0]上单调递减,则( )
| A、f(3)+f(4)>0 |
| B、f(-3)-f(-2)<0 |
| C、f(-2)+f(-5)<0 |
| D、f(4)-f(-1)>0 |
盒中装有6件产品,其中4件一等品,2件二等品,从中不放回的取两次,每次取一件,已知第二次取得一等品,则第一次取得的是二等品的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
则f(f(-2))( )
|
| A、16 | ||
B、
| ||
| C、4 | ||
D、
|
设sinα=
(
<α<π),tan(π-β)=
,则tan(α-2β)=( )
| 3 |
| 5 |
| π |
| 2 |
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|