题目内容
若函数f（x）是定义在[-6，6]的偶函数，且在[-6，0]上单调递减，则（ ）
| A、f（3）+f（4）＞0 |
| B、f（-3）-f（-2）＜0 |
| C、f（-2）+f（-5）＜0 |
| D、f（4）-f（-1）＞0 |
考点：函数单调性的性质
专题：函数的性质及应用
分析：根据偶函数在其对称的区间上的单调性相反可知选择A和D的真假，利用列举法可知选项B和选项C的真假，从而得到正确的结论．
解答：
解：∵函数f（x）是定义在[-6，6]上的偶函数，且在[-6，0]上单调递减
∴函数f（x）在[0，6]上的单调增函数
即f（4）-f（-1）＞0，f（-3）-f（-2）＜0
故D正确，B错
当f（x）=x2-16时选项a错误，当f（x）=x2时，选项C错误
故选：D．
∴函数f（x）在[0，6]上的单调增函数
即f（4）-f（-1）＞0，f（-3）-f（-2）＜0
故D正确，B错
当f（x）=x2-16时选项a错误，当f（x）=x2时，选项C错误
故选：D．
点评：本题主要考查了函数的奇偶性和单调性，以及列举法的运用，属于基础题．
练习册系列答案
一线名师提优试卷系列答案
相关题目
设m∈R，若函数f（x）=ex+2mx（x∈R）有大于零的极值点，则m的取值范围是（ ）
A、m＜-
| ||
| B、m＜0 | ||
C、m＞-
| ||
D、m＞
|
如图，是某算法流程图的一部分，其算法的逻辑结构为（ ）
| A、顺序结构 | B、条件结构 |
| C、判断结构 | D、循环结构 |
已知点A（1，1），B（3，3），则线段AB的垂直平分线的方程是（ ）
| A、y=-x+4 | B、y=x |
| C、y=x+4 | D、y=-x |
若A（x，1-x，2x），B（1，-2，x-1），当|
|取最小值时，x的值等于（ ）
| AB |
| A、1 | B、0 | C、-2 | D、-1 |
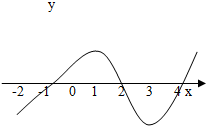如图是函数y=f（x）的导函数f′（x）的图象，对下列四个判断：①y=f（x）在（-2，-1）上是增函数；
②x=-1是极小值点；
③f（x）在（-1，2）上是增函数，在（2，4）上是减函数；
④x=3是f（x）的极小值点；
其中正确的是（ ）
| A、①② | B、③④ | C、②③ | D、②④ |
函数y=
的最大值是（ ）
| lnx |
| x |
| A、e |
| B、e-1 |
| C、e2 |
| D、e-2 |
从4名男生2名女生中，任选3名参加社区服务，则至少选到1名女生的概率是（ ）
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
下列各组向量中不平行的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|