题目内容
盒中装有6件产品，其中4件一等品，2件二等品，从中不放回的取两次，每次取一件，已知第二次取得一等品，则第一次取得的是二等品的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：概率的基本性质
专题：概率与统计
分析：第二次取得的是一等品的总的情况数：n=4×3+2×4=20种，第二次取得的是一等品，第一次取得二等品的情况数：m=2×4=8，根据古典概率公式第一次取得的是二等品的概率．
解答：
解：第二次取得的是一等品的总的情况数：n=4×3+2×4=20种
第二次取得的是一等品，第一次取得二等品的情况数：m=2×4=8，
根据古典概率公式第一次取得的是二等品的概率是：
P=
=
=
．
故选：D．
第二次取得的是一等品，第一次取得二等品的情况数：m=2×4=8，
根据古典概率公式第一次取得的是二等品的概率是：
P=
| m |
| n |
| 8 |
| 20 |
| 2 |
| 5 |
故选：D．
点评：本题考查概率的求法，是基础题，解题时要注意等可能事件概率计算公式的合理运用．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
相关题目
某算法的程序框图如图所示，则输出j的值是（ ）
| A、12 | B、11 | C、10 | D、9 |
若sin（
-x）=-
，则cos（
+x）的值等于（ ）
| π |
| 4 |
| 1 |
| 5 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知函数f（x）=2sin（ωx+
）（ω＞0），y=f（x）的图象与直线y=2的两个相邻交点的距离等于π，则f（x）的单调递增区间为（ ）
| π |
| 4 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
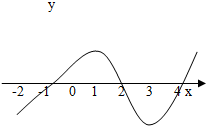如图是函数y=f（x）的导函数f′（x）的图象，对下列四个判断：①y=f（x）在（-2，-1）上是增函数；
②x=-1是极小值点；
③f（x）在（-1，2）上是增函数，在（2，4）上是减函数；
④x=3是f（x）的极小值点；
其中正确的是（ ）
| A、①② | B、③④ | C、②③ | D、②④ |
已知下列命题：
①命题“?x∈R，x2+1＞3x”的否定是“?x∈R，x2+1＜3x”；
②已知p、q为两个命题，若“p∨q”为假命题，则“￢p∧￢q”为真命题；
③命题p：0≤a＜1是命题q：0＜a＜5的既不充分又不必要条件；
④“若xy=0，则x=0且y=0”的逆否命题为真命题．
其中真命题的个数为（ ）
①命题“?x∈R，x2+1＞3x”的否定是“?x∈R，x2+1＜3x”；
②已知p、q为两个命题，若“p∨q”为假命题，则“￢p∧￢q”为真命题；
③命题p：0≤a＜1是命题q：0＜a＜5的既不充分又不必要条件；
④“若xy=0，则x=0且y=0”的逆否命题为真命题．
其中真命题的个数为（ ）
| A、3个 | B、2个 | C、1个 | D、0个 |
在△ABC中，角A、B、C的对边分别是a、b、c，若（cosC+ccosA）sinB=
b，则角B的值为（ ）
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在5件产品中，有3件正品和2件次品，从中任取2件，那么以
为概率的事件是（ ）
| 7 |
| 10 |
| A、都是正品 |
| B、至少有1件次品 |
| C、恰好有1件次品 |
| D、至多有1件次品 |