题目内容
若α∈(0,
),且sin2α+cos2α=
,则tanα的值等于( )
| π |
| 2 |
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:二倍角的余弦,同角三角函数间的基本关系
专题:三角函数的求值
分析:利用余弦的倍角公式对等式变形,利用平方关系得到正弦和余弦的比例式,再利用商数关系转化为正切的方程解之.
解答:
解:∵α∈(0,
),且sin2α+cos2α=
,
∴sin2α+cos2α-sin2α=
,
∴cos2α=
,
∴
=
,
∴
=
,
解得tanα=±
,
又∵α∈(0,
),
∴tanα=
.
故选:B.
| π |
| 2 |
| 3 |
| 4 |
∴sin2α+cos2α-sin2α=
| 3 |
| 4 |
∴cos2α=
| 3 |
| 4 |
∴
| cos2α |
| sin2α+cos2α |
| 3 |
| 4 |
∴
| 1 |
| tan2α+1 |
| 3 |
| 4 |
解得tanα=±
| ||
| 3 |
又∵α∈(0,
| π |
| 2 |
∴tanα=
| ||
| 3 |
故选:B.
点评:本题考查二倍角的余弦,同角三角函数间的基本关系的应用,考查计算能力.

练习册系列答案
相关题目
(lg2)20+C201(lg2)19lg5+…+C20r-1(lg2)21-r(lg5)r-1+…+(lg5)20=( )
| A、1 |
| B、(lg7)20 |
| C、220 |
| D、1020 |
以下说法错误的是( )
| A、零向量与任一非零向量平行 |
| B、平行向量方向相同 |
| C、零向量与单位向量的模不相等 |
| D、平行向量一定是共线向量 |
若sin(
-x)=-
,则cos(
+x)的值等于( )
| π |
| 4 |
| 1 |
| 5 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知点A(1,1),B(3,3),则线段AB的垂直平分线的方程是( )
| A、y=-x+4 | B、y=x |
| C、y=x+4 | D、y=-x |
已知函数f(x)=2sin(ωx+
)(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间为( )
| π |
| 4 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
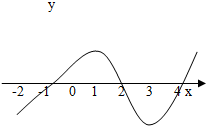 如图是函数y=f(x)的导函数f′(x)的图象,对下列四个判断:
如图是函数y=f(x)的导函数f′(x)的图象,对下列四个判断:①y=f(x)在(-2,-1)上是增函数;
②x=-1是极小值点;
③f(x)在(-1,2)上是增函数,在(2,4)上是减函数;
④x=3是f(x)的极小值点;
其中正确的是( )
| A、①② | B、③④ | C、②③ | D、②④ |
在△ABC中,角A、B、C的对边分别是a、b、c,若(cosC+ccosA)sinB=
b,则角B的值为( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将函数f(x)=sinx向左平移
个单位,得到函数y=g(x)的图象,则函数y=g(x)是( )
| π |
| 2 |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |