题目内容
袋子中有3个红球和2个黑球，从中摸出一个球，该球为黑球的概率是（ ）
A、
| ||
| B、1 | ||
C、
| ||
D、
|
考点：列举法计算基本事件数及事件发生的概率
专题：计算题,概率与统计
分析：列出所有基本事件即可求出概率．
解答：
解：设3个红球为a，b，c，和2个黑球为1，2；
则从中摸出一个球的所有基本事件有：a，b，c，1，2；共5种，
符合条件的有2种，故该球为黑球的概率P=
．
故选：C．
则从中摸出一个球的所有基本事件有：a，b，c，1，2；共5种，
符合条件的有2种，故该球为黑球的概率P=
| 2 |
| 5 |
故选：C．
点评：本题考查了基本事件的列法与概率的求法，属于基础题．
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
我们把正切函数在整个定义域内的图象看作一组“平行曲线”，而“平行曲线”具有性质：任意两条平行直线与两条相邻的“平行曲线”相交，被截得的线段长度相等．已知函数f（x）=tan（ωx+
）（ω＞0）图象中的两条相邻“平行曲线”与直线y=2013相交于A，B两点，且|AB|=2，f（
）=（ ）
| π |
| 3 |
| 1 |
| 2 |
A、2-
| ||||
B、-2-
| ||||
C、
| ||||
D、
|
（lg2）20+C201（lg2）19lg5+…+C20r-1（lg2）21-r（lg5）r-1+…+（lg5）20=（ ）
| A、1 |
| B、（lg7）20 |
| C、220 |
| D、1020 |
设m∈R，若函数f（x）=ex+2mx（x∈R）有大于零的极值点，则m的取值范围是（ ）
A、m＜-
| ||
| B、m＜0 | ||
C、m＞-
| ||
D、m＞
|
某算法的程序框图如图所示，则输出j的值是（ ）
| A、12 | B、11 | C、10 | D、9 |
函数y=2sinxcosx，x∈R的最小正周期是（ ）
A、
| ||
| B、π | ||
| C、2π | ||
D、
|
以下说法错误的是（ ）
| A、零向量与任一非零向量平行 |
| B、平行向量方向相同 |
| C、零向量与单位向量的模不相等 |
| D、平行向量一定是共线向量 |
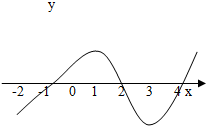如图是函数y=f（x）的导函数f′（x）的图象，对下列四个判断：