题目内容
已知平面向量
,
的夹角为
,且|
|=
,|
|=2,在△ABC中,
=2
+2
,
=2
-6
,D为BC中点,则|
|=( )
| m |
| n |
| π |
| 6 |
| m |
| 3 |
| n |
| AB |
| m |
| n |
| AC |
| m |
| n |
| AD |
| A、2 | B、4 | C、6 | D、8 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由已知中平面向量
,
的夹角为
,且|
|=
,|
|=2,
•
=3,再由D为边BC的中点,
=
(
+
)=2
-2
,利用平方法可求出
2=4,进而得到答案.
| m |
| n |
| π |
| 6 |
| m |
| 3 |
| n |
| m |
| n |
| AD |
| 1 |
| 2 |
| AB |
| AC |
| m |
| n |
| AD |
解答:
解:∵平面向量
,
的夹角为
,且|
|=
,|
|=2,
∴
•
=|
||
|cos
=3,
∵由D为边BC的中点,
∴
=
(
+
)=2
-2
,
∴
2=(2
-2
)2=4,
∴
|=2;
故选:A.
| m |
| n |
| π |
| 6 |
| m |
| 3 |
| n |
∴
| m |
| n |
| m |
| n |
| π |
| 6 |
∵由D为边BC的中点,
∴
| AD |
| 1 |
| 2 |
| AB |
| AC |
| m |
| n |
∴
| AD |
| m |
| n |
∴
| |AD |
故选:A.
点评:本题考查了平面向量数量积,向量的模,一般地求向量的模如果没有坐标,可以通过向量的平方求模.

练习册系列答案
相关题目
我们把正切函数在整个定义域内的图象看作一组“平行曲线”,而“平行曲线”具有性质:任意两条平行直线与两条相邻的“平行曲线”相交,被截得的线段长度相等.已知函数f(x)=tan(ωx+
)(ω>0)图象中的两条相邻“平行曲线”与直线y=2013相交于A,B两点,且|AB|=2,f(
)=( )
| π |
| 3 |
| 1 |
| 2 |
A、2-
| ||||
B、-2-
| ||||
C、
| ||||
D、
|
函数y=2sinxcosx,x∈R的最小正周期是( )
A、
| ||
| B、π | ||
| C、2π | ||
D、
|
以下说法错误的是( )
| A、零向量与任一非零向量平行 |
| B、平行向量方向相同 |
| C、零向量与单位向量的模不相等 |
| D、平行向量一定是共线向量 |
如图,是某算法流程图的一部分,其算法的逻辑结构为( )


| A、顺序结构 | B、条件结构 |
| C、判断结构 | D、循环结构 |
若sin(
-x)=-
,则cos(
+x)的值等于( )
| π |
| 4 |
| 1 |
| 5 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知点A(1,1),B(3,3),则线段AB的垂直平分线的方程是( )
| A、y=-x+4 | B、y=x |
| C、y=x+4 | D、y=-x |
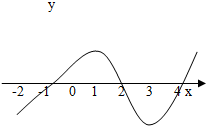 如图是函数y=f(x)的导函数f′(x)的图象,对下列四个判断:
如图是函数y=f(x)的导函数f′(x)的图象,对下列四个判断:①y=f(x)在(-2,-1)上是增函数;
②x=-1是极小值点;
③f(x)在(-1,2)上是增函数,在(2,4)上是减函数;
④x=3是f(x)的极小值点;
其中正确的是( )
| A、①② | B、③④ | C、②③ | D、②④ |
将5封信随意投入3个不同的邮箱里,每个邮箱中的信件不限,共有( )种不同的投法.
| A、5+3=8 |
| B、5×3=15 |
| C、53=125 |
| D、35=243 |